题目内容
14. 如图,已知⊙O的半径为3,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCPE是平行四边形,则AD的长为6.
如图,已知⊙O的半径为3,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCPE是平行四边形,则AD的长为6.
分析 连接BD,由ED为圆O的直径,利用直径所对的圆周角为直角得到∠DBE为直角,由BCOE为平行四边形,得到BC与OE平行,且BC=OE=3,在直角三角形ABD中,C为AD的中点,利用斜边上的中线等于斜边的一半求出AD的长即可.
解答 解:连接BD,
∵DE是直径,
∴∠DBE=90°,
∵四边形BCOE为平行四边形,
∴BC∥OE,BC=OE=3,
在Rt△ABD中,C为AD的中点,
∴BC=$\frac{1}{2}$AD=3,
∴AD=6,
故答案为6.
点评 此题考查了切线的判定与性质,直角三角形斜边上的中线性质,以及平行四边形的性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
相关题目
4.用平方差公式计算(x+1)(x2+1)(x-1)的结果正确的是( )
| A. | x4-1 | B. | x4+1 | C. | (x-1)4 | D. | (x+1)4 |
19.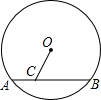 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )| A. | $\sqrt{13}$ | B. | 3 | C. | 4 | D. | 2$\sqrt{3}$ |
 数学课上,老师给同学编了如图所示的计算程序,当输入x的值是1时,输出的y的值是4.
数学课上,老师给同学编了如图所示的计算程序,当输入x的值是1时,输出的y的值是4.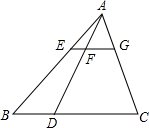 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.