题目内容
4. 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件∠ABC=90°时,四边形BEDF是正方形.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,DF∥AB,交BC于点F,当△ABC满足条件∠ABC=90°时,四边形BEDF是正方形.
分析 由题意知,四边形DEBF是平行四边形,再通过证明一组邻边相等,可知四边形DEBF是菱形,进而得出∠ABC=90°时,四边形BEDF是正方形.
解答 解:当△ABC满足条件∠ABC=90°,四边形DEBF是正方形.
理由:∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形
∵BD是∠ABC的平分线,
∴∠EBD=∠FBD,
又∵DE∥BC,
∴∠FBD=∠EDB,
则∠EBD=∠EDB,
∴BE=DE.
故平行四边形DEBF是菱形,
当∠ABC=90°时,
菱形DEBF是正方形.
故答案为:∠ABC=90°.
点评 本题主要考查了菱形、正方形的判定,正确掌握菱形以及正方形的判定方法是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.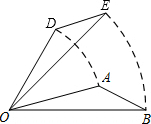 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
12.下列运算错误是( )
| A. | (a+b)2=a2+b2 | B. | a2•a3=a5 | C. | (a+b)(a-b)=a2-b2 | D. | 3a+4a=7a |
19.若x2+2(2p-3)x+4是完全平方式,则p的值等于( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | 2或1 | D. | $\frac{5}{2}$或$\frac{1}{2}$ |
 如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( )
如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( ) 如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.
如图,射线CF、AE与直线GH分别交于D、B,连接AD、CB,若∠HBE+∠GDC=180°,∠A=∠C,DA平分∠BDF.