题目内容
17．
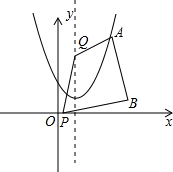如图，B为（4，1），点A（3，m）在抛物线y=（x-1）2+1上，点P是x轴上的一个动点，点Q是抛物线对称轴上的一个动点．则：（1）m=5，
（2）四边形ABPQ周长最小值为$\sqrt{61}$+$\sqrt{17}$．
分析 （1）把点A（3，m）代入y=（x-1）2+1，得到关于m的方程，解方程即可求得；
（2）由于线段AB为定长，故四边形ABPQ周长最小值即可转化为线段BP、PQ、QA和的最小值问题；作点A关于直线x=1的对称点A′，点B关于x轴对称点B′，连接A′B′，分别交直线x=1，x轴于点Q、P，则所作点Q、P即为所求．此时四边形ABPQ周长最小，最小值为AQ+PQ+PB+AB=A′Q+QP+PB′+AB=A′B′+AB，根据轴对称求得A′、B′的坐标，然后根据勾股定理求得AB、A′B′的长即可求得．
解答 
解：（1）∵点A（3，m）在抛物线y=（x-1）2+1上，
∴m=（3-1）2+1=5．
故答案为5．
（2）由于线段AB为定长，故四边形ABPQ周长最小值即可转化为线段BP、PQ、QA和的最小值问题．
如图，作点A关于直线x=1的对称点A′，点B关于x轴对称点B′，连接A′B′，分别交直线x=1，x轴于点Q、P，则所作点Q、P即为所求．此时四边形ABPQ周长最小，最小值为AQ+PQ+PB+AB=A′Q+QP+PB′+AB=A′B′+AB，
∵B（4，1），A（3，5），
∴A′（-1，5），B′（4，-1），AB=$\sqrt{（4-3）^{2}+（1-5）^{2}}$=$\sqrt{17}$
∴A′B′=$\sqrt{（4+1）^{2}+（-1-5）^{2}}$=$\sqrt{61}$，
∴四边形ABPQ周长最小值为：A′B′+AB=$\sqrt{61}$+$\sqrt{17}$．
故答案为$\sqrt{61}$+$\sqrt{17}$．
点评 本题考查了二次函数图象上点的坐标特征，轴对称的性质，轴对称-最短路线问题，勾股定理的应用等，（2）找出P、Q的位置是解题的关键，两点之间线段最短是轴对称问题的依据．
