题目内容
15. 如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.
如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.
分析 作DK∥AB交FC于K,根据题意得到△ADC的面积与△ABC的面积的关系,根据平行线分线段成比例定理得到$\frac{DG}{GA}$=$\frac{DK}{AF}$=$\frac{1}{6}$,得到△CDG的面积与△ADC的面积的关系,结合图形计算得到答案.
解答 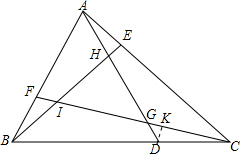 解:作DK∥AB交FC于K,
解:作DK∥AB交FC于K,
∵$\frac{DC}{DB}$=$\frac{1}{2}$,
∴△ADC的面积=$\frac{1}{3}$×△ABC的面积,
同理△ABE的面积=△BFC的面积=$\frac{1}{3}$×△ABC的面积,
∵DK∥AB,$\frac{DC}{DB}$=$\frac{1}{2}$,
∴$\frac{DK}{BF}$=$\frac{1}{3}$,又$\frac{FB}{FA}$=$\frac{1}{2}$,
∴$\frac{DK}{AF}$=$\frac{1}{6}$,
∵DK∥AB,
∴$\frac{DG}{GA}$=$\frac{DK}{AF}$=$\frac{1}{6}$,
∴△CGD的面积=$\frac{1}{7}$×△ADC的面积=$\frac{1}{21}$×△ABC的面积,
同理,△BFI的面积=△AEH的面积═$\frac{1}{21}$×△ABC的面积,
∴△GHID的面积+3×$\frac{1}{3}$×△ABC的面积=△ABC的面积+3×$\frac{1}{21}$×△ABC的面积,
∴$\frac{△GHI的面积}{△ABC的面积}$=$\frac{1}{7}$.
点评 本题考查的是平行线分线段成比例定理和三角形面积的计算,灵活运用平行线分线段成比例定理、找准对应关系、理解等高的两个三角形的面积之比等于两底的比是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.方程x(x+3)=k(x+3)有一个根为正数,则k满足的条件是( )
| A. | k>0 | B. | k<0 | C. | k≠0 | D. | 以上答案都不对 |
4.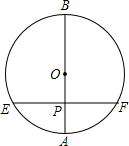 如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
 如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )
如图所示,在⊙O中,直径AB⊥弦EF,垂足为P,AP=1cm,BP=3cm,EF等于( )| A. | 2$\sqrt{3}$cm | B. | $\sqrt{3}$cm | C. | 2cm | D. | 4cm |
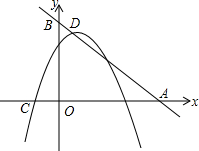 如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3) 如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由.
如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由. 如图,以AD为边的三角形是△ABD,△ADC,以∠B为内角的三角形是△ABD,△ABC,△ACD的三个内角分别是∠ACD,∠ADC,∠CAD;三边分别是AC,AD,CD.
如图,以AD为边的三角形是△ABD,△ADC,以∠B为内角的三角形是△ABD,△ABC,△ACD的三个内角分别是∠ACD,∠ADC,∠CAD;三边分别是AC,AD,CD.