题目内容
若直角三角形中，斜边的长为13，一条直角边长为5，则这个三角形的面积是（ ）
| A、60 | B、30 | C、20 | D、32 |
考点：勾股定理
专题：
分析：设另一直角边为x，根据勾股定理求出x的值，再根据三角形的面积公式即可得出结论．
解答：解：设另一直角边为x，
∵斜边的长为13，一条直角边长为5，
∴x=
=12，
∴S=
×5×12=30．
故选B．
∵斜边的长为13，一条直角边长为5，
∴x=
| 132-52 |
∴S=
| 1 |
| 2 |
故选B．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
已知?ABCD的周长为32，AB=4，则BC=（ ）| A、8 | B、12 | C、24 | D、28 |
平面直角坐标系中，点（1，-2）在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
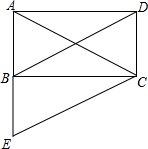如图，在矩形ABCD中，将△ABD沿AB向下平移使A点到达B点，得到△BEC，下列说法正确的是（ ）| A、△ACE一定是等腰三角形 |
| B、△ACE一定是等边三角形 |
| C、△ACE一定是锐角三角形 |
| D、△ACE不可能是等腰直角三角形 |
如图，在一个平行四边形中，两对平行于边的直线将这个平行四边形分为九个小平行四边形，如果原来这个平行四边形的面积为100cm2，而中间那个小平行四边形（阴影部分）的面积为20平方厘米，则四边形ABDC的面积是（ ）| A、40cm2 |
| B、60cm2 |
| C、70cm2 |
| D、80cm2 |
如图，P是⊙O的直径AB延长线上一点，PC切⊙O于C，∠P=50°，∠A为（ ）| A、40° | B、35° |
| C、25° | D、20° |
已知三角形的两边分别是5和10，则此三角形的第三边长可能是（ ）
| A、4 | B、5 | C、9 | D、16 |