题目内容
15．志愿者服务站为指导农民发展种植业进行技术培训，三期共培训95人，其中第一期培训20人，求每期培训人数的平均增长率，设平均增长率为x，根据题意列出的方程为（ ）| A． | 20（1+x）2=95 | B． | 20（1+x）3=95 | ||
| C． | 20（1+x）+20（1+x）2=95 | D． | 20（1+x）+20（1+x）2=95-20 |
分析 设平均增长率为x，根据第一期培训了20人，可得出第二、三期培训人数，根据三期共培训人数=第一期培训人数+第二期培训人数+第三期培训人数，即可得出关于x的一元二次方程，此题得解．
解答 解：设平均增长率为x，则第二期培训20（1+x）人，第三期培训20（1+x）2人，
根据题意得：20+20（1+x）+20（1+x）2=95．
故选D．
点评 本题考查了由时间问题抽象出一元二次方程，找准等量关系，列出一元二次方程是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．
如图所示，△ABC的各个顶点都在正方形的格点上，则sinA的值为（ ）
如图所示，△ABC的各个顶点都在正方形的格点上，则sinA的值为（ ）| A． | $\frac{\sqrt{10}}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{2\sqrt{10}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
10．下列运算正确的是（ ）
| A． | （-2a3）2=-4a6 | B． | $\sqrt{9}$=±3 | C． | m2•m3=m6 | D． | x5+2x5=3x5 |
20．下列计算中错误的有（ ）
①4a3b÷2a2=2a，②-12x4y3÷2x2y=6x2y2，③-16a2bc÷$\frac{1}{4}$a2b=-4c，④（-$\frac{1}{2}$ab2）3÷（-$\frac{1}{2}$ab2）=$\frac{1}{4}$a2b4．
①4a3b÷2a2=2a，②-12x4y3÷2x2y=6x2y2，③-16a2bc÷$\frac{1}{4}$a2b=-4c，④（-$\frac{1}{2}$ab2）3÷（-$\frac{1}{2}$ab2）=$\frac{1}{4}$a2b4．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．
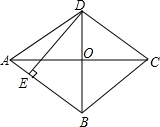如图，菱形ABCD的对角线AC，BD交于点O，AC=8，BD=6，DE⊥AB于点E，则DE的长为（ ）
如图，菱形ABCD的对角线AC，BD交于点O，AC=8，BD=6，DE⊥AB于点E，则DE的长为（ ）| A． | $\frac{12}{5}$ | B． | $\frac{24}{5}$ | C． | 6 | D． | 4 |
4．下列等式成立的是（ ）
| A． | $\sqrt{27}$=3$\sqrt{3}$ | B． | -（-$\frac{1}{2}$）=-$\frac{1}{2}$ | C． | 3+$\sqrt{3}$=3$\sqrt{3}$ | D． | （a2）3=a5 |
5．下列计算正确的是（ ）
| A． | x2+x2=x4 | B． | xy4÷（-xy）=-y3 | C． | （x+y）2=x2+y2 | D． | x3•x2=x6 |