题目内容
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(-1,-1),(0,0),(
,
),…都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数y=
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足-2<x1<2,|x1-x2|=2,令t=b2-2b+
,试求出t的取值范围.
| 2 |
| 2 |
(1)若点P(2,m)是反比例函数y=
| n |
| x |
(2)函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足-2<x1<2,|x1-x2|=2,令t=b2-2b+
| 157 |
| 48 |
考点:二次函数综合题
专题:代数综合题,压轴题,新定义
分析:(1)先由“梦之点”的定义得出m=2,再将点P坐标代入y=
,运用待定系数法即可求出反比例函数的解析式;
(2)假设函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”(x,x),则有x=3kx+s-1,整理得(3k-1)x=1-s,再分三种情况进行讨论即可;
(3)先将A(x1,x1),B(x2,x2)代入y=ax2+bx+1,得到ax12+(b-1)x1+1=0,ax22+(b-1)x2+1=0,根据方程的解的定义可知x1,x2是一元二次方程ax2+(b-1)x+1=0的两个根,由根与系数的关系可得x1+x2=
,x1•x2=
,则(x1-x2)2=(x1+x2)2-4x1•x2=
=4,整理得出b2-2b=(2a+1)2-2,则t=b2-2b+
=(2a+1)2+
.再由-2<x1<2,|x1-x2|=2,得出-4<x2<4,-8<x1•x2<8,即-8<
<8,又a>0,解不等式组得出a>
,进而求出t的取值范围.
| n |
| x |
(2)假设函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”(x,x),则有x=3kx+s-1,整理得(3k-1)x=1-s,再分三种情况进行讨论即可;
(3)先将A(x1,x1),B(x2,x2)代入y=ax2+bx+1,得到ax12+(b-1)x1+1=0,ax22+(b-1)x2+1=0,根据方程的解的定义可知x1,x2是一元二次方程ax2+(b-1)x+1=0的两个根,由根与系数的关系可得x1+x2=
| 1-b |
| a |
| 1 |
| a |
| b2-2b+1-4a |
| a2 |
| 157 |
| 48 |
| 61 |
| 48 |
| 1 |
| a |
| 1 |
| 8 |
解答:解:(1)∵点P(2,m)是“梦之点”,
∴m=2,
∵点P(2,2)在反比例函数y=
(n为常数,n≠0)的图象上,
∴n=2×2=4,
∴反比例函数的解析式为y=
;
(2)假设函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”(x,x),
则有x=3kx+s-1,
整理,得(3k-1)x=1-s,
当3k-1≠0,即k≠
时,解得x=
;
当3k-1=0,1-s=0,即k=
,s=1时,x有无穷多解;
当3k-1=0,1-s≠0,即k=
,s≠1时,x无解;
综上所述,当k≠
时,“梦之点”的坐标为(
,
);当k=
,s=1时,“梦之点”有无数个;当k=
,s≠1时,不存在“梦之点”;
(3)∵二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),
∴x1=ax12+bx1+1,x2=ax22+bx2+1,
∴ax12+(b-1)x1+1=0,ax22+(b-1)x2+1=0,
∴x1,x2是一元二次方程ax2+(b-1)x+1=0的两个不等实根,
∴x1+x2=
,x1•x2=
,
∴(x1-x2)2=(x1+x2)2-4x1•x2=(
)2-4•
=
=4,
∴b2-2b=4a2+4a-1=(2a+1)2-2,
∴t=b2-2b+
=(2a+1)2-2+
=(2a+1)2+
.
∵-2<x1<2,|x1-x2|=2,
∴-4<x2<0或0<x2<4,
∴-4<x2<4,
∴-8<x1•x2<8,
∴-8<
<8,
∵a>0,
∴a>
∴(2a+1)2+
>
+
=
,
∴t>
.
∴m=2,
∵点P(2,2)在反比例函数y=
| n |
| x |
∴n=2×2=4,
∴反比例函数的解析式为y=
| 4 |
| x |
(2)假设函数y=3kx+s-1(k,s是常数)的图象上存在“梦之点”(x,x),
则有x=3kx+s-1,
整理,得(3k-1)x=1-s,
当3k-1≠0,即k≠
| 1 |
| 3 |
| 1-s |
| 3k-1 |
当3k-1=0,1-s=0,即k=
| 1 |
| 3 |
当3k-1=0,1-s≠0,即k=
| 1 |
| 3 |
综上所述,当k≠
| 1 |
| 3 |
| 1-s |
| 3k-1 |
| 1-s |
| 3k-1 |
| 1 |
| 3 |
| 1 |
| 3 |
(3)∵二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),
∴x1=ax12+bx1+1,x2=ax22+bx2+1,
∴ax12+(b-1)x1+1=0,ax22+(b-1)x2+1=0,
∴x1,x2是一元二次方程ax2+(b-1)x+1=0的两个不等实根,
∴x1+x2=
| 1-b |
| a |
| 1 |
| a |
∴(x1-x2)2=(x1+x2)2-4x1•x2=(
| 1-b |
| a |
| 1 |
| a |
| b2-2b+1-4a |
| a2 |
∴b2-2b=4a2+4a-1=(2a+1)2-2,
∴t=b2-2b+
| 157 |
| 48 |
| 157 |
| 48 |
| 61 |
| 48 |
∵-2<x1<2,|x1-x2|=2,
∴-4<x2<0或0<x2<4,
∴-4<x2<4,
∴-8<x1•x2<8,
∴-8<
| 1 |
| a |
∵a>0,
∴a>
| 1 |
| 8 |
∴(2a+1)2+
| 61 |
| 48 |
| 25 |
| 16 |
| 61 |
| 48 |
| 17 |
| 6 |
∴t>
| 17 |
| 6 |
点评:本题是二次函数的综合题,考查了运用待定系数法求反比例函数的解析式,形如ax=b的方程的解的情况,一元二次方程根与系数的关系,不等式的性质等知识,综合性较强,有一定难度.

练习册系列答案
相关题目
 如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=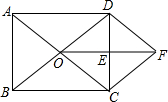 已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证: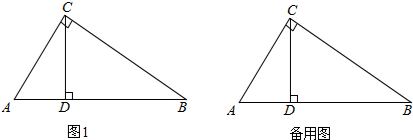
 如图,
如图,