题目内容
已知一个样本1,3,2,2,a,b,c的众数为3,平均数为2,则该样本的方差为 .
考点:方差,算术平均数,众数
专题:
分析:因为众数为3,表示3的个数最多,因为2出现的次数为二,所以3的个数最少为三个,则可设a,b,c中有两个数值为3.另一个未知利用平均数定义求得,从而根据方差公式求方差.
解答:解:解:因为众数为3,可设a=3,b=3,c未知,
平均数=
(1+3+2+2+3+3+c)=2,
解得c=0,
根据方差公式S2=
[(1-2)2+(3-2)2+(2-2)2+(2-2)2+(3-2)2+(3-2)2+(0-2)2]=
;
故答案为:
.
平均数=
| 1 |
| 7 |
解得c=0,
根据方差公式S2=
| 1 |
| 7 |
| 8 |
| 7 |
故答案为:
| 8 |
| 7 |
点评:本题考查了方差和众数、平均数,关键是掌握众数是出现次数最多的数.

练习册系列答案
相关题目
已知x,y满足关系式2x+y=9和x+2y=6,则x+y=( )
| A、6 | B、-1 | C、15 | D、5 |
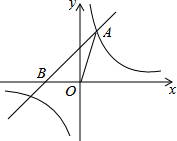 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)