题目内容
6.解分式方程:$\frac{5x-96}{x-19}$+$\frac{x-8}{x-9}$=$\frac{4x-19}{x-16}$+$\frac{2x-21}{x-8}$.分析 首先将原方程变为:(5-$\frac{1}{x-19}$)+(1$+\frac{1}{x-9}$)=(4$+\frac{5}{x-6}$)+(2+$\frac{5}{x-8}$),然后再移项、合并同类项得到:$\frac{1}{x-9}-\frac{1}{x-19}=\frac{5}{x-6}+\frac{5}{x-8}$,然后将等号左右两边分别通分得:∴$\frac{-10}{(x-9)(x-19)}=\frac{-10}{(x-8)(x-6)}$,然后去分母得:(x-6)(x-8)=(x-9)(x-19),然后即可求得原方程的解.
解答 解:原方程可变形为:(5-$\frac{1}{x-19}$)+(1$+\frac{1}{x-9}$)=(4$+\frac{5}{x-6}$)+(2+$\frac{5}{x-8}$)
整理得:$\frac{1}{x-9}-\frac{1}{x-19}=\frac{5}{x-6}+\frac{5}{x-8}$,
∴$\frac{-10}{(x-9)(x-19)}=\frac{-10}{(x-8)(x-6)}$.
∴(x-6)(x-8)=(x-9)(x-19)
整理得:14x=123,
解得:x=$\frac{123}{14}$,
经检验x=$\frac{123}{14}$是原方程的解.
所以原方程的解为x=$\frac{123}{14}$.
点评 本题主要考查的是解分式方程,如何将该分式方程转化整式方程是解题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
17.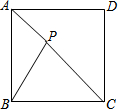 如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
 如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
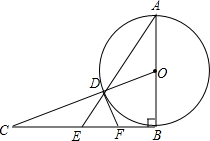 如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.
如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.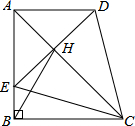 在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( )
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的个数是( ) 如图,四边形ABCD的四个顶点的坐标分别为A(-2,2),B(-4,-3),C(3,-3),D(2,1),求四边形ABCD的面积.
如图,四边形ABCD的四个顶点的坐标分别为A(-2,2),B(-4,-3),C(3,-3),D(2,1),求四边形ABCD的面积.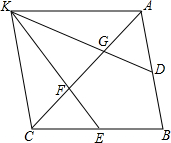 已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.
已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.