题目内容
11.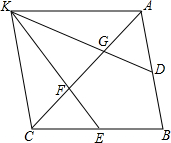 已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.
已知△ABC,D,E分别为AB,BC上的中点,F,G为AC的三等分点.连接EF,DG交于K.连接AK,CK,求证:四边形ABCK为平行四边形.
分析 首先延长KE、AB相交于M,连接BG,根据D,E分别为AB,BC上的中点,F,G为AC的三等分点可得$\frac{KG}{DG}$=$\frac{CG}{AG}$,然后可证出△CKG∽△ADG,根据相似三角形的性质可得∠DAG=∠KCG,$\frac{KC}{AD}=\frac{KG}{DG}$=2,进而可得KC∥AB,KC=2AD=AB,根据一组对边平行且相等的四边形是平行四边形可得结论.
解答 证明:延长KE、AB相交于M,连接BG,
∵CF=FG,CE=BE,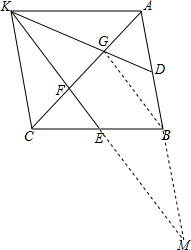
∴EF∥BG,
∵AG=FG,
∴MB=AB=2BD,
∵BG∥EF,
∴BG∥KM,
∴$\frac{KG}{DG}$=$\frac{BM}{BD}$=2,
而$\frac{CG}{AG}$=2,
∴$\frac{KG}{DG}$=$\frac{CG}{AG}$,
∴△CKG∽△ADG,
∴∠DAG=∠KCG,$\frac{KC}{AD}=\frac{KG}{DG}$=2,
∴KC∥AB,KC=2AD=AB,
∴四边形ABCK为平行四边形.
点评 此题主要考查了平行四边形的判定,以及相似三角形的判定与性质,关键是正确证明△CKG∽△ADG.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知mn<0,$\frac{1}{m^2}+\frac{1}{n^2}$=1,化简m$\sqrt{1-\frac{1}{m^2}}-n\sqrt{1-\frac{1}{n^2}}$以后得到的结果是( )
| A. | mn或-mn | B. | -mn | C. | mn | D. | 2 |
16.若(x+3)(2x-m)=2x2+x-15,则实数m的值( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
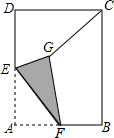 如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.
如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.