Question

12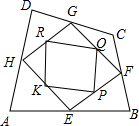．如图，铎山中心学校校园内有一块四边形空地ABCD，学校征集对这块空地种植的花草的设计中，选定如下方案：把这个四边形分成九块，种植三种不同的花草，其中E、F、G、H分别是AB、BC、CD、DA的中点，P、Q、R、K分别是EF、FG、GH、HE的中点，现要在四边形PQRK中种上红色的花，在△PFQ、△QGR、△RHK、△KEP中种上黄色的花，在△HAE、△EBF、△FCG、△GDH中种上紫色的花．已知种红、黄、紫三种花的单价分别为10元/m²、12元/m²、14元/m²，而种红花已用去了120元．请你用学过的数学知识计算出种满四边形ABCD这块空地的花共需要多少元？

Answer 1

分析 先根据三角形的中位线得出：S_△DHG+S△_BEF+S_△AEH+S_△CFG=$\frac{1}{2}$S_{四边形ABCD}，即种紫色花的面积是四边形ABCD面积的一半，同理得出：种黄色花的面积是四边形EFGH面积的一半；再根据种红花已用去了120元和单价为10元/m²计算出种红花的面积，则得出种黄和紫花的面积，最后根据各自的单价得出种满四边形ABCD这块空地的花共需要的钱数．

解答 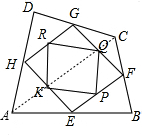解：连结AC，可知HG是△DAC的中位线，
∴△DHG∽△DAC，
∴S_△DHG=$\frac{1}{4}$S_△DAC，
同理S_△BEF=$\frac{1}{4}$S_△BAC，
∴S_△DHG+S_△BEF=$\frac{1}{4}$S_△DAC+$\frac{1}{4}$S_△BAC=$\frac{1}{4}$S_{四边形ABCD}，
同理S_△AEH+S_△CFG=$\frac{1}{4}$S_{四边形ABCD}，
∴S_△DHG+S△_BEF+S_△AEH+S_△CFG，
=$\frac{1}{4}$S_{四边形ABCD}+$\frac{1}{4}$S_{四边形ABCD}，
=$\frac{1}{2}$S_{四边形ABCD}，
即种紫色花的面积是四边形ABCD面积的一半，
同理：种黄色花的面积是四边形EFGH面积的一半，
∴种黄色花的面积与种红色花的面积相等，种紫色花的面积是种红色花的面积的两倍，
可知种红色花的面积是：120÷10=12㎡，
故种黄色花的面积是12㎡，种紫色花的面积是24㎡，
∴种满四边形ABCD这块空地的花共需要：120+12×12+14×24=600元．

点评 本题是中点四边形，通过连接对角线构建三角形，运用三角形中位线的性质：三角形的中位线平行于第三边，且等于第三边的一半；可知平行相似且面积比是相似比的平方，从而得出种三种花所占面积的关系．