题目内容
4.已知抛物线C1的函数解析式为y=ax2-2x-3a,若抛物线C1经过点(0,-3).(1)求抛物线C1的顶点坐标.
(2)已知实数x>0,请证明x+$\frac{1}{x}$≥2,并说明x为何值时才会有x+$\frac{1}{x}$=2;
(3)若将抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线C2,设A(m,y1),B(n,y2)是C2上的两个不同点,且满足:∠AOB=90°,m>0,n<0.请你用含m的表达式表示出△AOB的面积S,并求出S的最小值及S取最小值时一次函数OA的函数解析式.
(参考公式:在平面直角坐标系中,若P(x1,y1),Q(x2,y2),则P,Q两点间的距离为$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$)
分析 (1)利用待定系数法求解析式,配方成顶点式后写出顶点坐标即可;
(2)利用平方的非负性可知:x+$\frac{1}{x}$-2=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2≥0,移项可得结论;
(3)如图所示,根据平移的原则得出C2的解析式为:y=x2则A(m,m2),B(n,n2),利用勾股定理列式得:OA2+OB2=AB2,即m2+m4+n2+n4=(m-n)2+(m2-n2)2化简得:m n=-1,代入面积公式:S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$$\sqrt{{m}^{2}+{m}^{4}}$•$\sqrt{{n}^{2}+{n}^{4}}$,$\frac{1}{2}$(m+$\frac{1}{m}$)≥$\frac{1}{2}$×2=1,从而得出结论.
解答 解:(1)∵抛物线过(0,-3)点,
∴-3a=-3,
∴a=1,
∴y=x2-2x-3,
∴y=x2-2x-3=(x-1)2-4,
∴抛物线C1的顶点坐标为(1,-4);
(2)∵x>0,
∴x+$\frac{1}{x}$-2=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2≥0,
∴x+$\frac{1}{x}$≥2,
显然当x=1时,才有x+$\frac{1}{x}$=2;
(3)如图所示,由平移知识易得C2的解析式为:y=x2,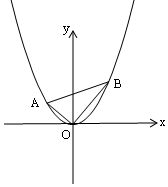
∴A(m,m2),B(n,n2),
∵△AOB为Rt△,
∴OA2+OB2=AB2,
∴m2+m4+n2+n4=(m-n)2+(m2-n2)2化简得:m n=-1,
∵S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$$\sqrt{{m}^{2}+{m}^{4}}$•$\sqrt{{n}^{2}+{n}^{4}}$,
∵m n=-1,
∴S△AOB=$\frac{1}{2}$$\sqrt{2+{m}^{2}+{n}^{2}}$=$\frac{1}{2}$$\sqrt{2+{m}^{2}+\frac{1}{{m}^{2}}}$=$\frac{1}{2}$$\sqrt{(m+\frac{1}{m})^{2}}$=$\frac{1}{2}$(m+$\frac{1}{m}$)≥$\frac{1}{2}$×2=1,
∴S△AOB的最小值为1,此时m=1,A(1,1),
∴直线OA的一次函数解析式为y=x.
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、抛物线平移的原则、平方的非负性、三角形面积及两点间距离公式的应用,难度适中.

 名校课堂系列答案
名校课堂系列答案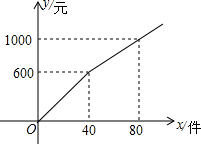 梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )
梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系的图象如图所示,则降价后每件商品销售的价格为( )| A. | 5元 | B. | 15元 | C. | 12.5元 | D. | 10元 |
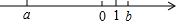 在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )
在数轴上,实数a,b对应的点的位置如图所示,下列结论中,正确的是( )| A. | |a|<1 | B. | |a|>1 | C. | |b|<1 | D. | ab>0 |
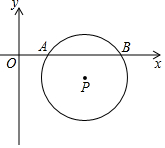 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2$\sqrt{3}$.将⊙P向上平移,当⊙P与x轴相切时平移的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3 |
| A. | 圆锥体 | B. | 圆柱体 | C. | 球体 | D. | 长方体 |
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,点A坐标为(3,4),点E在线段OC上,点F在线段BC上,且满足∠BEF=∠AOC.