题目内容
2.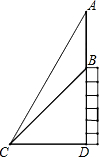 如图,楼顶有一根天线AB,为了测量天线的高度,在地面点C处测得楼顶B点的仰角∠BCD为45°,测得天线顶点A的仰角∠ACD为60°,且点C到楼的距离CD为15米,求天线AB的长(结果保留根号).
如图,楼顶有一根天线AB,为了测量天线的高度,在地面点C处测得楼顶B点的仰角∠BCD为45°,测得天线顶点A的仰角∠ACD为60°,且点C到楼的距离CD为15米,求天线AB的长(结果保留根号).
分析 根据已知条件求出CD=BD=15米,再根据在Rt△AC中,AD=tan60°•CD,求出AD的值,最后根据AB=AD-BD,即可得出答案.
解答 解:∵Rt△BCD中,∠BCD=45°,
∴∠CBD=45°,
∴CD=BD,
∵CD=15米,
∴BD=15米,
Rt△AC中,∠ACD=60°,
∴tan60°=$\frac{AD}{CD}$,
∴AD=tan60°•CD=15$\sqrt{3}$,
∴AB=AD-BD=15$\sqrt{3}$-15(米),
∴天线AB的长(15$\sqrt{3}$-15)米.
点评 本题考查仰角的定义,以及解直角三角形的实际应用问题.此题难度不大,解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形,注意当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.

练习册系列答案
相关题目
11.计算(a+2b)2的结果是( )
| A. | a2+4b2 | B. | a2+2ab+2b2 | C. | a2+4ab+2b2 | D. | a2+4ab+4b2 |
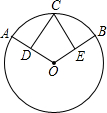 如图,在⊙O中,$\widehat{AC}=\widehat{BC}$,点D、E分别在半径OA和OB上,AD=BE.求证:CD=CE.
如图,在⊙O中,$\widehat{AC}=\widehat{BC}$,点D、E分别在半径OA和OB上,AD=BE.求证:CD=CE.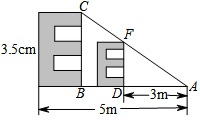 为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计的方案新颖,构思巧妙.甲生的方案:根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?
为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计的方案新颖,构思巧妙.甲生的方案:根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?