题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
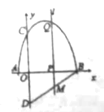
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]()
(2)当![]() ,四边形
,四边形![]() 是平行四边形
是平行四边形
(3)存在,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]()
【解析】
(1)根据函数解析式列方程即可;
(2)根据平行四边形的判定,用含未知数的值表示QM的长度,从而可求解;
(3)设Q点的坐标为![]() ,分两种情况讨论:
,分两种情况讨论:![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]() ,
,![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]() ,可解出
,可解出![]() 的值.
的值.
(1)令![]() ,则
,则![]() ,C点的坐标为(0,2);
,C点的坐标为(0,2);
令![]() ,则
,则![]() 解得
解得![]() ,点A为(-1,0);点B为(4,0)
,点A为(-1,0);点B为(4,0)
∴![]()
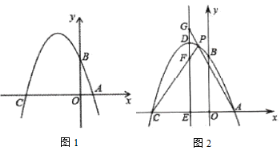
(2)如图1所示:
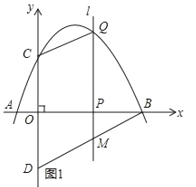
点C与点D关于![]() 轴对称,点
轴对称,点![]() ,设直线BD的解析式为
,设直线BD的解析式为![]() ,将
,将![]() 代入得:
代入得:![]() 解得
解得![]()
∴直线BD的解析式为:![]()
∵![]()
∴当![]() 时,四边形
时,四边形![]() 是平行四边形
是平行四边形
设Q点的坐标为![]() ,则
,则![]()
∴![]()
解得![]()
![]() (不合题意,舍去)
(不合题意,舍去)
∴当![]() ,四边形
,四边形![]() 是平行四边形
是平行四边形
(3)存在,设Q点的坐标为![]()
∵![]() 是以BD为直角边的直角三角形
是以BD为直角边的直角三角形
∴![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得:![]()
即![]()
解得![]()
![]() (不合题意,舍去)
(不合题意,舍去)
∴Q点的坐标为![]()
![]() 当
当![]() 时,由勾股定理可得:
时,由勾股定理可得: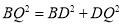
即![]()
解得![]()
![]()
Q点的坐标为![]()
![]()
综上所述:点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() .
.

【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
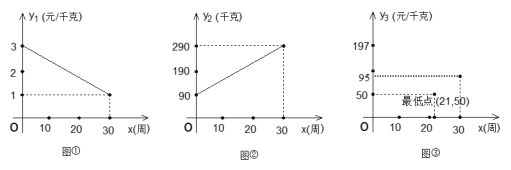
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?