题目内容
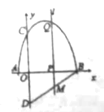
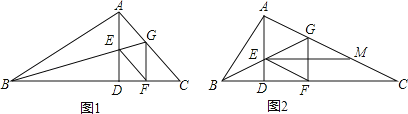
【题目】在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC于F,连接EF.
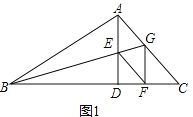
(1)如图1,求证:四边形AEFG是菱形;
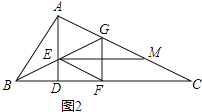
(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长![]() 倍的所有线段.
倍的所有线段.
【答案】(1)见解析;(2)是CM长![]() 倍的所有线段有AB、BF、CF、EM.
倍的所有线段有AB、BF、CF、EM.
【解析】
(1)先证明四边形AEFG是平行四边形,再证明AE=AG即可.
(2)先证明AB=![]() AG,再分别证明AB=BF=CF=EM,CM=AG即可.
AG,再分别证明AB=BF=CF=EM,CM=AG即可.
(1)证明:∵AD⊥BC,GF⊥BC,
∴∠ADF=∠GFC=90![]() ,
,
∴AE∥GF,
在△ABG和△FBG中,
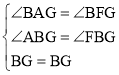 ,
,
∴△ABG≌△FBG,
∴AG=FG,
∵∠FBG+∠BED=90![]() ,
,
∵∠BED=∠AEG,
∴∠FBG+∠AEG=90![]() ,
,
∵∠ABG+∠AGE=90![]() ,
,
∵∠ABG=∠FBG,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=FG,
∴四边形AEFG是平行四边形,
∵AE=AG∴四边形AEFG是菱形.
(2)解:∵四边形AEFG是菱形,
∴AE=AG,
∵BE=EG,∠BAG=90![]() ,
,
∴AE=BE=EG,
∴△AEG是等边三角形,
∴∠AGE=60![]() ,
,
在RT△ABG中,∵∠ABG=30![]() ,
,
∴AB=AG÷cos30![]() =
=![]() AG,
AG,
∵∠C=30![]() ,
,
∴BC=2AB,
∴BE=GE,EF∥AC,EM∥BC,
∴BF=FC,CM=GM,
在RT△AEM中,∵∠AME=∠C=30![]() ,∠GEM+∠GME=60
,∠GEM+∠GME=60![]() ,
,
∴∠GEM=∠GME=30![]() ,
,
∴EG=AG=GM=CM,
∵EM∥FC,EF∥CM,
∴四边形EFCM是平行四边形,
∴AB=BF=CF=EM=![]() CM,
CM,
∴是CM ![]() 倍的所有线段有AB、BF、CF、EM.
倍的所有线段有AB、BF、CF、EM.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.