题目内容
17.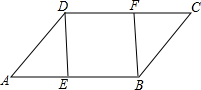 如图,在?ABCD中,点E,F分别在AB,CD上,AE=CF.
如图,在?ABCD中,点E,F分别在AB,CD上,AE=CF.(1)求证:DE=BF;
(2)求证:四边形DEBF是平行四边形.
分析 (1)利用平行四边形的性质得出AB∥CD,AB=CD,进而求出BE=DF,进而利用一组对边平行且相等的四边形是平行四边形,证出平行四边形,得出对边相等即可;
(2)利用平行四边形的性质得出AB∥CD,AB=CD,进而求出BE=DF,进而利用一组对边平行且相等的四边形是平行四边形进而证出即可.
解答 (1)证明:在?ABCD中,AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∴DE=BF;
(2)证明:在?ABCD中,AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形.
点评 此题主要考查了平行四边形的判定与性质;熟记一组对边平行且相等的四边形是平行四边形,得出BE=DF是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )
 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1+∠4=180° | D. | ∠4=∠5 |
6.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
| A. | C,r | B. | C,π,r | C. | C,πr | D. | C,2π,r |
7.现在宁波市的出租车的起步价为10元(行驶不超过3.5千米),以后每增加1千米,加价2元,每趟另加2元燃油附加费.现在某人乘出租车行驶s千米的路程(s>3.5)所需的费用是( )
| A. | 12+2s | B. | 10+2(s+1) | C. | 12+2s-3.5 | D. | 12+2(s-3.5) |
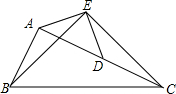 如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.
如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.