题目内容
请观察下列算式,找出规律并填空
=1-
,
=
-
,
=
-
,
=
-
则:
(1)第10个算式是 = ;
(2)第n个算式为 = ;
(3)根据以上规律解答下题:1+
+
+
+…+
的值.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)第10个算式是
(2)第n个算式为
(3)根据以上规律解答下题:1+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
考点:有理数的混合运算
专题:规律型
分析:(1)观察一系列等式确定出第10个等式即可;
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的拆项方法计算即可.
(2)归纳总结得到一般性规律,写出即可;
(3)利用得出的拆项方法计算即可.
解答:解:(1)第10个算式是
=
-
;
(2)第n个算式为
=
-
;
(3)根据以上规律解答下题:1+
+
+
+…+
=1+1-
=1
.
故答案为:(1)
,
-
;(2)
,
-
;
| 1 |
| 10×11 |
| 1 |
| 10 |
| 1 |
| 11 |
(2)第n个算式为
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(3)根据以上规律解答下题:1+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
故答案为:(1)
| 1 |
| 10×11 |
| 1 |
| 10 |
| 1 |
| 11 |
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
点评:此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
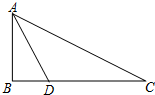 如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.
如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.