Question

19．已知，如图，l₁∥l₂．

（1）如图1，过点P作l₁的平行线，可证∠APB，∠A，∠B之间的等量关系是：∠APB=∠A+∠B．
（2）如图2，请你写出∠APB，∠A，∠B之间的等量关系，并证明．
（3）如图3，请你直接写出∠P₁，∠P₂，∠P₃，∠P₄，∠P₅之间的等量关系为：∠P₂+∠P₄+∠P₅=∠P₁+∠P₃+180°．

Answer 1

分析 （1）过P作PE∥l₁，根据平行线的性质和角的和差即可得到结论；
（2）过点P作PQ∥l₁，根据平行线的性质和等量代换即可得到结论；
（3）分别过P₂，P₃，P₄作P₂A∥l₁，P₃B∥l₁，P₄C∥l₁，根据平行线的性质和角的和差即可得到结论．

解答 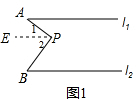解：（1）过P作PE∥l₁，
∵l₁∥l₂，
∴l₂PE∥l₁，
∴∠A=∠1，∠B=∠2，
∴∠APB=∠1+∠2=∠A+∠B；

（2）等量关系为：∠APB-∠A+∠B=180°，
证明：过点P作PQ∥l₁，
∵PQ∥l₁，
∴∠A=∠1，
∵l₁∥l₂，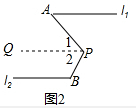
∴PQ∥l₂，
∴∠2+∠B=180°，
∴∠2=180°-∠B，
∵∠2=∠APB-∠1，
∴∠APB-∠1=180°-∠B，
∵∠A=∠1，
∴∠APB-∠A=180°-∠B，
∴∠APB-∠A+∠B=180°；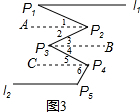

（3）如图3，分别过P₂，P₃，P₄作P₂A∥l₁，P₃B∥l₁，P₄C∥l₁，
∵l₁∥l₂，
∴l₁P₂A∥P₃B∥P₄C，
∴∠P₁=∠1，∠2=∠3，∠4=∠5，∠6+∠P₅=180°，
∴∠P₂+∠P₄+∠P₅=∠P₁+∠P₃+180°．
故答案为：∠P₂+∠P₄+∠P₅=∠P₁+∠P₃+180°．

点评 本题考查了培训的性质，熟练掌握平行线的性质是解题的关键．