题目内容
15.如果方程组$\left\{\begin{array}{l}{x+y=8}\\{y+z=6}\\{z+x=4}\end{array}\right.$的解使代数式kx+2y-3z的值为8,则k=( )| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
分析 先求出方程组的解,再根据方程组$\left\{\begin{array}{l}{x+y=8}\\{y+z=6}\\{z+x=4}\end{array}\right.$的解使代数式kx+2y-3z的值为8,可以求得k的值,本题得以解决.
解答 解:$\left\{\begin{array}{l}{x+y=8}&{①}\\{y+z=6}&{②}\\{z+x=4}&{③}\end{array}\right.$
①-②,得
x-z=2④
③+④,得
2x=6,
解得,x=3
将x=3代入①,得
y=5,
将x=3代入③,得
z=1,
故原方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=5}\\{z=1}\end{array}\right.$,
又∵方程组$\left\{\begin{array}{l}{x+y=8}\\{y+z=6}\\{z+x=4}\end{array}\right.$的解使代数式kx+2y-3z的值为8,
∴3k+2×5-3×1=8,
解得,k=$\frac{1}{3}$,
故选A.
点评 本题考查解三元一次方程组,解题的关键是明确三元一次方程组的解法.

练习册系列答案
相关题目
3.若$\sqrt{x+3}$=3,则(x+3)2的平方根是( )
| A. | 81 | B. | ±81 | C. | ±9 | D. | ±3 |
20.下列各运算中,计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (-3ab2)2=9a2b4 | D. | (a-b)2=a2-b2 |
7.下列命题中真命题的个数是( )
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
①两条对角线相等的四边形是矩形 ②菱形是中心对称图形,不是轴对称图形
③对角线互相垂直且相等的四边形是正方形 ④依次连结矩形各边的中点,所得四边形是菱形.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.下列各式属于最简二次根式是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{4}$ | C. | $\sqrt{6}$ | D. | $\sqrt{8}$ |
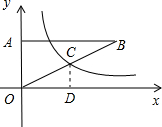 如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.
如图,在平面直角坐标系中,Rt△AOB的直角顶点A在y轴的正半轴上,顶点B在第一象限,函数y=$\frac{k}{x}$的图象与边OB交于点C,且点C为边OB的中点.若△AOB的面积为12,则k的值为6.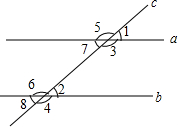 如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )
如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是( )