题目内容
已知:直线y=-x+m与坐标轴交于M、N两点,点B在NM的延长线上,OC⊥OB,且OC=OB,OG⊥BC于G交MN于点A.
(1)如图1,连NC,求证:△OCN≌△OBM;
(2)如图2,在条件(1)下,过A点作AE⊥y轴,过B点作BF⊥x轴,垂足分别为E、F,EA、BF的延长线相交于P点,求证:AE2+BF2=AP2.
(3)如图3,当m=2时,在条件(2)下,双曲线y=
经过点P,求k的值.

(1)如图1,连NC,求证:△OCN≌△OBM;
(2)如图2,在条件(1)下,过A点作AE⊥y轴,过B点作BF⊥x轴,垂足分别为E、F,EA、BF的延长线相交于P点,求证:AE2+BF2=AP2.
(3)如图3,当m=2时,在条件(2)下,双曲线y=
| k |
| x |

考点:反比例函数综合题
专题:综合题
分析:(1)对于直线y=-x+m,分别令x与y为0求出y与x的值,得到OM=ON,再由OB与OC垂直,OM与ON垂直,利用垂直的定义得到一对直角相等,利用等式的性质得到一对角相等,再由OB=OC,利用SAS得到三角形ONC与三角形OMB全等即可;
(2)利用两对角相等的三角形相似得到三角形AOB与三角形NOB,利用相似得比例列出关系式,设AE=a,BF=b,AP=c,OE=t,根据三角形NOM与三角形BPA都为等腰三角形,得到t=m-a=c-b,即m+b=c+a,根据勾股定理列出关系式,整理即可得证;
(3)设B(g,2-g)(g>0),则得到C坐标为(g-2,g),表示出中点G坐标,确定出直线OG解析式,与直线MN解析式联立求出A的坐标,进而确定出P坐标,即可求出k的值.
(2)利用两对角相等的三角形相似得到三角形AOB与三角形NOB,利用相似得比例列出关系式,设AE=a,BF=b,AP=c,OE=t,根据三角形NOM与三角形BPA都为等腰三角形,得到t=m-a=c-b,即m+b=c+a,根据勾股定理列出关系式,整理即可得证;
(3)设B(g,2-g)(g>0),则得到C坐标为(g-2,g),表示出中点G坐标,确定出直线OG解析式,与直线MN解析式联立求出A的坐标,进而确定出P坐标,即可求出k的值.
解答: (1)证明:对于直线y=-x+m,
(1)证明:对于直线y=-x+m,
令x=0,得到y=m;令y=0,得到x=m,即OM=ON,
∵OB⊥OC,OM⊥ON,
∴∠BOC=∠MON=90°,
∴∠BOC-∠COM=∠NOM-∠COM,即∠NOC=∠MOB,
在△NOC和△MOB中,
,
∴△NOC≌△MOB(SAS);
(2)解:∵△MON,△BOC为等腰直角三角形,G为BC中点,
∴∠BOA=∠BNO=45°,
∵∠OBN为公共角,
∴△BOA∽△BNO,
∴
=
,即BO2=BA•BN,
设AE=a,BF=b,AP=c,OE=t,
∵△NOM和△BPA都为等腰三角形,
∴t=m-a=c-b,即m+b=c+a,
在Rt△OFB中,根据勾股定理得:OB2=(b+m)2+b2=(c+a)2+b2,
∵BA=
c,BN=
(c+a),
∴c2=a2+b2,即AE2+BF2=AP2;
(3)解:设B(g,2-g)(g>0),
过C作CS⊥y轴,过B作BH⊥y轴,
∵∠SOC+∠BOH=90°,∠SOC+∠SCO=90°,
∴∠BOH=∠SCO,
在△SOC和△HBO中,
,
∴△SOC≌△HBO(AAS),
∴CS=OH=g-2,SO=HB=g,
∴点C可表示为(g-2,g),
∴BC中点G坐标为(g-1,1),
∴直线OG解析式为y=
x,
与直线MN:y=-x+2,联立得:
,
消去y得:
x=-x+2,
解得:x=
,
将x=
代入得:y=
•
=
,
∴A(
,
),
∴P(g,
),
则k=2.
 (1)证明:对于直线y=-x+m,
(1)证明:对于直线y=-x+m,令x=0,得到y=m;令y=0,得到x=m,即OM=ON,
∵OB⊥OC,OM⊥ON,
∴∠BOC=∠MON=90°,
∴∠BOC-∠COM=∠NOM-∠COM,即∠NOC=∠MOB,
在△NOC和△MOB中,
|
∴△NOC≌△MOB(SAS);
(2)解:∵△MON,△BOC为等腰直角三角形,G为BC中点,
∴∠BOA=∠BNO=45°,
∵∠OBN为公共角,
∴△BOA∽△BNO,
∴
| BO |
| BN |
| AB |
| BO |
设AE=a,BF=b,AP=c,OE=t,
∵△NOM和△BPA都为等腰三角形,
∴t=m-a=c-b,即m+b=c+a,
在Rt△OFB中,根据勾股定理得:OB2=(b+m)2+b2=(c+a)2+b2,
∵BA=
| 2 |
| 2 |
∴c2=a2+b2,即AE2+BF2=AP2;
(3)解:设B(g,2-g)(g>0),
过C作CS⊥y轴,过B作BH⊥y轴,
∵∠SOC+∠BOH=90°,∠SOC+∠SCO=90°,
∴∠BOH=∠SCO,
在△SOC和△HBO中,
|
∴△SOC≌△HBO(AAS),
∴CS=OH=g-2,SO=HB=g,
∴点C可表示为(g-2,g),
∴BC中点G坐标为(g-1,1),
∴直线OG解析式为y=
| 1 |
| g-1 |
与直线MN:y=-x+2,联立得:
|
消去y得:
| 1 |
| g-1 |
解得:x=
| 2g-2 |
| g |
将x=
| 2g-2 |
| g |
| 1 |
| g-1 |
| 2g-2 |
| g |
| 2 |
| g |
∴A(
| 2g-2 |
| g |
| 2 |
| g |
∴P(g,
| 2 |
| g |
则k=2.
点评:此题属于反比例函数综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,两直线的交点坐标,以及反比例函数的图象与性质,熟练掌握反比例函数的性质是解本题的关键.

练习册系列答案
相关题目
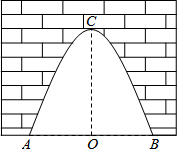 如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.
如图:某古城有一个抛物线形石拱门,拱门地面的最大宽度AB=4米,拱门的最大高度OC=4米.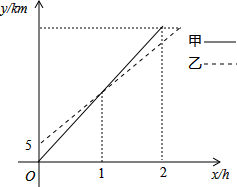 在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图.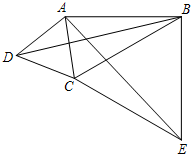 如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.