题目内容
利用二次函数图象求x2+5x-3=0的近似根(精确到0.1)
考点:图象法求一元二次方程的近似根
专题:
分析:根据二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.
解答: 解:方程x2+5x-3=0根是函数y=x2+5x-3与x轴交点的横坐标.
解:方程x2+5x-3=0根是函数y=x2+5x-3与x轴交点的横坐标.
作出二次函数y=x2+5x-3的图象,如图所示,
由图象可知方程有两个根,一个在-6和-5之间,另一个在0和1之间.
先求0和1之间的根,
当x=0.5时,y=-0.25;当x=0.6时,y=0.36;
因此,x=0.5是方程的一个近似根,
同理,x=-5.5是方程的另一个近似根.
故x2+5x-3=0的近似根为x=0.5或-5.5.
 解:方程x2+5x-3=0根是函数y=x2+5x-3与x轴交点的横坐标.
解:方程x2+5x-3=0根是函数y=x2+5x-3与x轴交点的横坐标.作出二次函数y=x2+5x-3的图象,如图所示,
由图象可知方程有两个根,一个在-6和-5之间,另一个在0和1之间.
先求0和1之间的根,
当x=0.5时,y=-0.25;当x=0.6时,y=0.36;
因此,x=0.5是方程的一个近似根,
同理,x=-5.5是方程的另一个近似根.
故x2+5x-3=0的近似根为x=0.5或-5.5.
点评:本题考查了图象法求一元二次方程的近似根,二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.

练习册系列答案
相关题目
下列比较大小正确的是( )
A、-
| ||||
| B、π-4<-2 | ||||
| C、-(-2)3<0 | ||||
| D、-2<-5 |
下列各数中,最小的数是( )
| A、-3 | ||
B、-
| ||
| C、2 | ||
| D、0 |
如图所示,不可能围成正方体的是( )
A、 |
B、 |
C、 |
D、 |
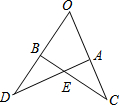 如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )
如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )| A、130° | B、85° |
| C、105° | D、95° |
X<0,Y>0时,则X,X+Y,X-Y,Y中最小的数是( )
| A、X-Y | B、Y | C、X+Y | D、X |
 将图中的硬纸盘按虚线折叠,可以围成怎样的几何体.
将图中的硬纸盘按虚线折叠,可以围成怎样的几何体.