题目内容
7．已知m为有理数，则当m=1时，式子（m-1）2+$\frac{5}{4}$的值最小，最小值为$\frac{5}{4}$．分析 根据非负数的性质解答即可．
解答 解：∵（m-1）2≥0，
∴m-1=0，即m=1时，式子（m-1）2+$\frac{5}{4}$的值最小，最小值为$\frac{5}{4}$．
故答案为：1，$\frac{5}{4}$．
点评 本题考查的是非负数的性质，熟知任意一个数的偶次方都是非负数是解答此题的关键．
练习册系列答案
相关题目
17．下列合并同类项，结果正确的是（ ）
| A． | x4+x4=x8 | B． | 5m-2m+4m=7m | ||
| C． | 15a+4a-11=18a | D． | -9xy-2xy+11xy=xy |
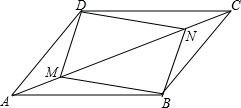已知：如图，在平行四边形ABCD中，点M，N在对角线AC上，且AM=CN．求证：四边形BMDN是平行四边形．
如图，已知∠1=∠2，DE=CE，∠AEB=90°，求证：∠3=∠4．
2．计算-$\frac{2}{5}$+（$\frac{5}{8}$$-\frac{1}{6}$$+\frac{7}{12}$）×（-2.4）的结果是（ ）
| A． | -2.9 | B． | 2.9 | C． | -2.8 | D． | 2.8 |
如图所示，M是梯形ABCD的腰CD的中点，MN⊥AB，垂足为N．求证：S△ABM=$\frac{1}{2}$梯形ABCD．
设有两个非负数a、b．则有如下证明：∵（$\sqrt{a}$-$\sqrt{b}$）2≥0（当且仅当a=b时等号成立）．∴a-2$\sqrt{ab}$+b≥0．∴a+b≥2$\sqrt{ab}$，∴$\sqrt{ab}$≤$\frac{a+b}{2}$（或ab≤$\frac{（a+b）^{2}}{4}$）（当且仅当a=b时等号成立）根据这一证明的结论解答下列问题：