题目内容
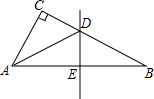 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,ED是AB的垂直平分线,则BD=
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,ED是AB的垂直平分线,则BD=考点:线段垂直平分线的性质
专题:
分析:根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,利用勾股定理列式求出BC,设BD=AD=x,表示出CD,然后在Rt△ACD中,利用勾股定理列出方程计算即可得解.
解答:解:∵ED是AB的垂直平分线,
∴AD=BD,
∵∠C=90°,AC=3,AB=5,
∴BC=
=
=4,
设BD=AD=x,则CD=4-x,
在Rt△ACD中,AD2=AC2+CD2,
即x2=32+(4-x)2,
解得x=
,
即BD=
.
故答案为:
.
∴AD=BD,
∵∠C=90°,AC=3,AB=5,
∴BC=
| AB2-AC2 |
| 52-32 |
设BD=AD=x,则CD=4-x,
在Rt△ACD中,AD2=AC2+CD2,
即x2=32+(4-x)2,
解得x=
| 25 |
| 8 |
即BD=
| 25 |
| 8 |
故答案为:
| 25 |
| 8 |
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,勾股定理的应用,熟记性质并在Rt△ACD中列出方程是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
下列长度的三根小木棒能构成三角形的是( )
| A、3,5,10 |
| B、5,5,10 |
| C、5,4,8 |
| D、8,2,3 |
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,直至得C14,若P(41,m)在这列抛物线上,则m=
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,直至得C14,若P(41,m)在这列抛物线上,则m=