题目内容
直线y=-2x-6与两坐标轴围成的三角形的面积为 .
考点:一次函数图象上点的坐标特征
专题:
分析:分别令x=0,y=0求出直线与坐标轴的交点,再根据三角形的面积公式解答即可.
解答:解:令x=0,则y=-6,
令y=0,则x=-3,
故直线y=2x+6与两坐标轴的交点分别为(0,-6)、(-3,0),
故两坐标轴围成的三角形面积=
×|-3|×|-6|=9.
故答案为:9.
令y=0,则x=-3,
故直线y=2x+6与两坐标轴的交点分别为(0,-6)、(-3,0),
故两坐标轴围成的三角形面积=
| 1 |
| 2 |
故答案为:9.
点评:本题考查的是一次函数图象上点的坐标特点,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
下列命题是真命题的是( )
| A、90°的直角所对的弦是直径 |
| B、平分弦的直径垂直于这条弦 |
| C、同圆或等圆中等弧所对圆周角相等 |
| D、一条弦把圆分成的两段弧中,至少有一段是优弧 |
方程x(x+2)=x+2的两根分别为( )
| A、x1=-1,x2=2 |
| B、x1=1,x2=2 |
| C、x1=-1,x2=-2 |
| D、x1=1,x2=-2 |
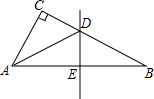 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,ED是AB的垂直平分线,则BD=
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,ED是AB的垂直平分线,则BD=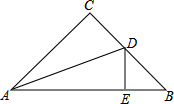 如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于
如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于