题目内容
 如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2且AC:BD=2:3,求平行四边形ABCD的面积.
如图,平行四边形ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2且AC:BD=2:3,求平行四边形ABCD的面积.考点:平行四边形的性质
专题:
分析:由四边形ABCD是平行四边形,可得OA=
AC,OB=
BD,由AC:BD=2:3,可得OA:OB=2:3,又由AC⊥AB,AB=2,利用勾股定理即可求得各线段的长,继而求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵四边形ABCD是平行四边形,
∴OA=
AC,OB=
BD,
∵AC:BD=2:3,
∴OA:OB=2:3,
设OA=2x,OB=3x,
∵AC⊥AB,AB=2,
∴AB2+OA2=OB2,
∴4+(2x)2=(3x)2,
解得:x=
,
∴AC=2OA=4x=
,
∴S?ABCD=AB•AC=
.
∴OA=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC:BD=2:3,
∴OA:OB=2:3,
设OA=2x,OB=3x,
∵AC⊥AB,AB=2,
∴AB2+OA2=OB2,
∴4+(2x)2=(3x)2,
解得:x=
2
| ||
| 5 |
∴AC=2OA=4x=
8
| ||
| 5 |
∴S?ABCD=AB•AC=
16
| ||
| 5 |
点评:此题考查了平行四边形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、等腰三角形 | B、菱形 |
| C、平行四边形 | D、直角三角形 |
在直角坐标系中,要将图形向左平移3个单位时,只需( )
| A、将图形上的每个点的横坐标减3,纵坐标不变 |
| B、将图形上的每个点的横坐标加3,纵坐标不变 |
| C、将图形上的每个点的横坐标不变,纵坐标减3 |
| D、将图形上的每个点的横坐标不变,纵坐标加3 |
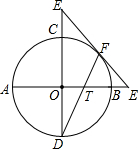 如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=
如图,AB和CD是互相垂直的两条直径,E为DC延长线上一点,EF切⊙O于点F,交AB的延长线于H,DF交AB于T,若tan∠D=