题目内容
6.一个矩形的对角线长为6,对角线与一边的夹角是45°,求这个矩形的各边长.分析 由矩形的性质得出AB=CD,BC=AD,∠A=90°,BD=6,由已知条件得出△ABD是等腰直角三角形,由三角函数求出AB=AD=$\frac{\sqrt{2}}{2}$BD,即可得出AB=BC=CD=AD=3$\sqrt{2}$.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴AB=CD,BC=AD,∠BAD=90°,AC=BD=6,
∵∠ABD=45°,
∴△ABD是等腰直角三角形,
∴AB=AD=$\frac{\sqrt{2}}{2}$BD=$\frac{\sqrt{2}}{2}$×6=3$\sqrt{2}$,
∴AB=BC=CD=AD=3$\sqrt{2}$.
点评 本题考查了矩形的性质、等腰直角三角形的判定与性质、三角函数;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知三角形的两边分别为3和7,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 10 |
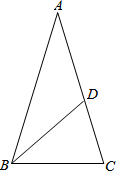 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC.