题目内容
17.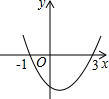 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2-4ac>0;④8a+c>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2-4ac>0;④8a+c>0.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 ①因为点(-1,0),(3,0)在二次函数上,所以a-b+c=0,9a+3b+c=0,两式作差可得8a+4b=0,故2a+b=0,则①正确;
②由图形可知,该二次函数的a>0,c<0,顶点的横坐标-$\frac{b}{2a}$=1>0,则b<0,知abc>0,故②错误;
③函数图象与x轴两个交点,可知b2-4ac>0,故③正确;
④由图象可知$-\frac{b}{2a}=1$,则b=-2a,因(3,0)在函数图象上,故9a+3b+c=0,将b=-2a代入得3a+c=0,由函数图象知a>0,故3a+c+5a>0,即8a+c>0.故④正确.
解答 解:A.①因为点(-1,0),(3,0)在二次函数上,所以a-b+c=0,9a+3b+c=0,两式作差可得8a+4b=0,故2a+b=0,则①正确;②由图形可知,该二次函数的a>0,c<0,顶点的横坐标-$\frac{b}{2a}$=1>0,则b<0,知abc>0,故②错误;
③函数图象与x轴两个交点,可知b2-4ac>0,故③正确;
④由图象可知$-\frac{b}{2a}=1$,则b=-2a,因(3,0)在函数图象上,故9a+3b+c=0,将b=-2a代入得3a+c=0,由函数图象知a>0,故3a+c+5a>0,即8a+c>0.故④正确.
故选项A正确;
B.①因为点(-1,0),(3,0)在二次函数上,所以a-b+c=0,9a+3b+c=0,两式作差可得8a+4b=0,故2a+b=0,则①正确;
②由图形可知,该二次函数的a>0,c<0,顶点的横坐标-$\frac{b}{2a}$=1>0,则b<0,知abc>0,故②错误;
③函数图象与x轴两个交点,可知b2-4ac>0,故③正确;
④由图象可知$-\frac{b}{2a}=1$,则b=-2a,因(3,0)在函数图象上,故9a+3b+c=0,将b=-2a代入得3a+c=0,由函数图象知a>0,故3a+c+5a>0,即8a+c>0.故④正确.
故选项B错误;
C.①因为点(-1,0),(3,0)在二次函数上,所以a-b+c=0,9a+3b+c=0,两式作差可得8a+4b=0,故2a+b=0,则①正确;
②由图形可知,该二次函数的a>0,c<0,顶点的横坐标-$\frac{b}{2a}$=1>0,则b<0,知abc>0,故②错误;
③函数图象与x轴两个交点,可知b2-4ac>0,故③正确;
④由图象可知$-\frac{b}{2a}=1$,则b=-2a,因(3,0)在函数图象上,故9a+3b+c=0,将b=-2a代入得3a+c=0,由函数图象知a>0,故3a+c+5a>0,即8a+c>0.故④正确.
故选项C错误;
D.①因为点(-1,0),(3,0)在二次函数上,所以a-b+c=0,9a+3b+c=0,两式作差可得8a+4b=0,故2a+b=0,则①正确;
②由图形可知,该二次函数的a>0,c<0,顶点的横坐标-$\frac{b}{2a}$=1>0,则b<0,知abc>0,故②错误;
③函数图象与x轴两个交点,可知b2-4ac>0,故③正确;
④由图象可知$-\frac{b}{2a}=1$,则b=-2a,因(3,0)在函数图象上,故9a+3b+c=0,将b=-2a代入得3a+c=0,由函数图象知a>0,故3a+c+5a>0,即8a+c>0.故④正确.
故选项D错误.
故选A.
点评 本题考查学生对二次函数图象与系数的理解,并且会巧妙的对一些式子进行变形得到想要的结论.

| A. | y=$\frac{1}{x+2}$ | B. | y=4x | C. | y=$\frac{2}{3x}$ | D. | y=$\frac{7}{x^2}$ |
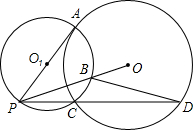 如图,P是⊙O外一点,PA切⊙O于点A,PA为直径作⊙O1,交PO于点B,交⊙O于点C,连结PC并延长交⊙O于点D.连结BD.
如图,P是⊙O外一点,PA切⊙O于点A,PA为直径作⊙O1,交PO于点B,交⊙O于点C,连结PC并延长交⊙O于点D.连结BD.