题目内容
16．
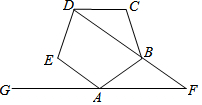如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA=36°．
分析 首先求得正五边形内角∠C的度数，然后根据CD=CB求得∠CDB的度数，然后利用平行线的性质求得∠DFA的度数即可．
解答 解：∵正五边形的外角为360°÷5=72°，
∴∠C=180°-72°=108°，
∵CD=CB，
∴∠CDB=36°，
∵AF∥CD，
∴∠DFA=∠CDB=36°．
故答案为：36°．
点评 本题考查了多边形的内角和外角及平行线的性质，解题的关键是求得正五边形的内角．
练习册系列答案
相关题目
18．
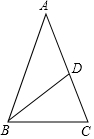如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）
如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）| A． | 36° | B． | 60° | C． | 108° | D． | 72° |
1．
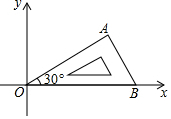将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）
将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，-$\sqrt{3}$） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，$\sqrt{2}$） |
8．
如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（ ）
如图，是直立在高速公路边水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为（ ）| A． | 4$\sqrt{3}$米 | B． | （2$\sqrt{3}$+2）米 | C． | （4$\sqrt{2}$-4）米 | D． | （4$\sqrt{3}$-4）米 |
6．若抛物线的图象经过A（0，3），B（2，0），C（0，-2），D（5，3）中的三个点，则关于该抛物线的叙述正确的是（ ）
| A． | 不经过点A | B． | 不经过点B | ||
| C． | 开口向下 | D． | 顶点为（2.5，-0.125） |