题目内容
11.已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+m的图象相交于点(2,1).(1)分别求出这两个函数的解析式;
(2)试判断点P(-1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
分析 (1)把点的坐标代入反比例函数和一次函数的一般式即可求出函数解析式.
(2)首先根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,求出点P(-1,5)关于x轴的对称点P′的坐标,再代入一次函数解析式,看看是否满足解析式,满足则在一次函数y=kx+m的图象上,反之则不在.
解答 解:(1)∵点(2,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴1=$\frac{k}{2}$,
解得k=2.
∴y=$\frac{2}{x}$为所求反比例函数的解析式.
又∵点(2,1)在一次函数y=kx+b的图象上,
∴1=2×2+b,
解得b=-3,
∴y=2x-3为所求的一次函数解析式.
综上所述,反比例函数为y=$\frac{2}{x}$,一次函数为y=2x-3;
(2)点P(-1,5)关于x轴的对称点P′的坐标是(-1,-5),
把(-1,-5)代入y=2x-3中,
-5=2×(-1)-3,
∴点P′在一次函数y=2x-3的图象上.
点评 此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式,关键是把握住凡是图象经过的点都能满足解析式.

练习册系列答案
相关题目
6.在反比例函数y=$\frac{4}{x}$的图象中,阴影部分的面积等于4的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
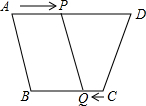 梯形ABCD中AD∥BC且AB=DC,AD=10cm,BC=6cm,P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,Q以4cm/s的速度由C出发向B运动,问:
梯形ABCD中AD∥BC且AB=DC,AD=10cm,BC=6cm,P、Q分别从A、C同时出发,P以2cm/s的速度由A向D运动,Q以4cm/s的速度由C出发向B运动,问: