题目内容
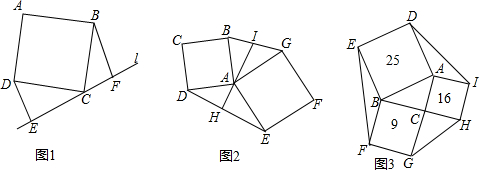
2.(1)如图1,直线l经过正方形ABCD的顶点C,分别过点D、B作l的垂线段DE、BF.求证:△DCE≌△CBF(2)将上述的图形作为一个“基本图形”,你能否在下列的问题中构建这样的“基本图形”解决问题:
如图2,正方形ABCD与正方形AEFG有共同的顶点A,连接DE、BG,过点A作直线AH⊥DE,交BG于点I,求证:I是BG的中点.
(3)通过(2)的证明:我们可以发现上图中S△ADE=S△ABG(填“>”、“<”、或“=”).并利用你的发现解决下列问题:如图3,以△ABC的各边为一边向外作正方形,各正方形的面积如图中所示,分别为9、16、25,请直接写出六边形DEFGHI的面积:74.
分析 (1)根据全等三角形的判定证明即可;
(2)由(1)可知:△DAH≌△ABM,△EAH≌△AGN,从而可知:BM=AH=GN,然后再证明△BIM≌△GIN,从而可得到BI=BI;
(3)由全等三角形的性质可知S△ADE=S△ABG,然后用上述结论可知△BEF、△GCH,△ADI的面积都等于△ACB的面积,从而可求得答案.
解答 证明:(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCB=90°,
∴∠DCE+∠BCF=90°,
∵DE⊥CE,BF⊥CF,
∴∠DCE+∠EDC=90°,
∴∠BCF=∠EDC,
同理∠DCE=∠CBF,
在△DCE与△CBF中,
$\left\{\begin{array}{l}{∠DCE=∠CBF}\\{∠BCF=∠EDC}\\{DC=BC}\end{array}\right.$,
∴△DCE≌△CBF(AAS);
(2)过点B作BM⊥AI于点M,过点G作GN⊥AI交延长线于点N,
由(1)可知:△DAH≌△ABM、△AHE≌△GNA,
∴BM=AH,GN=AH.
∴BM=GN.
在△BMI和△GNI中,
$\left\{\begin{array}{l}{∠BMA=∠GNA}\\{∠BMI=∠GNI}\\{BM=NG}\end{array}\right.$,
∴△BMI≌△GNI.
∴BI=GI.
(3)∵△DAH≌△ABM、△AHE≌△GNA,
∴S△ADE=S△ABM+S△ANG.
∵△BMI≌△GNI,
∴S△BMI=S△GNI.
∴S△ADE=S△ABG.
∴${S}_{△BEF}={S}_{△CGH}={S}_{△ADI}={S}_{△ABC}=\frac{1}{2}×3×4=6$.
∴六边形的面积=25+16+9+4×6=74.
点评 本题主要考查的是全等三角形的性质和判定,发现问题的结论,并利用问题的结论进行证明是解题的关键.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.
若点O为直线AB上一点,OC为射线,OE平分∠AOC,OF平分∠BOC.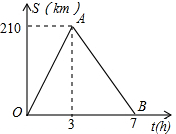 小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.
小明从A地出发,途中经过C地,后到达B地,到达B地后,立即原路返回,他距A地的距离S(千米)和所用时间t(小时)之间的函数关系如图所示,若小明前后两次经过点C时间相差2$\frac{1}{3}$小时,那么A、C两地之间距离为140千米.