题目内容
9．
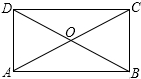如图，在矩形ABCD中，对角线AC，BD相交于O，∠AOB=120°，AD=3，那么对角线AC的长是6．
分析 根据矩形的对角线相等且互相平分可得OA=OD，再求出∠AOD=60°，然后判断出△AOD是等边三角形，根据等边三角形的性质求出OA，即可得出AC的长．
解答 解：在矩形ABCD中，OA=OC=$\frac{1}{2}$AC，OB=OD=$\frac{1}{2}$BD，AC=BD，
∴OA=OD，
∵∠AOB=120°，
∴∠AOD=180°-120°=60°，
∴△AOD是等边三角形，
∴OA=AD=3，
∴AC=2OA=6；
故答案为：6．
点评 本题考查了矩形的性质，等边三角形的判定与性质，熟记矩形的性质，证出△AOD是等边三角形是解题的关键．
练习册系列答案
相关题目
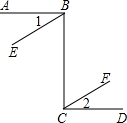如图，直线AB和直线CD，直线BE和直线CF都被直线BC所截，在下面三个式子只，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并写出对应的推理过程
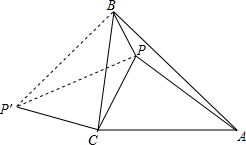如图，△ABC中，∠ACB=90°，AC=BC，P是△ABC内的一点，且AP=3，CP=2，BP=1，求∠BPC得度数．（提示：把△CAP绕点C逆时针旋转90°到△CBP′，证明△BPP′为Rt△）