题目内容
1.解下列方程(1)$\left\{\begin{array}{l}{x-y=4}\\{2x+y=5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x-y=-4}\\{4x-5y=-23}\end{array}\right.$
(3)$\left\{\begin{array}{l}{3(x-1)=2y-2}\\{5(y-1)=2(x+10)}\end{array}\right.$
(4)$\left\{\begin{array}{l}{13x+14y=41}\\{14x+13y=40}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组两方程相加得到x+y=3,与第一个方程联立,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=4①}\\{2x+y=5②}\end{array}\right.$,
①+②得:3x=9,即x=3,
把x=3代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x-y=-4①}\\{4x-5y=-23②}\end{array}\right.$,
①×2-②得:3y=15,即y=5,
把y=5代入①得:x=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=5}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{3x-2y=1①}\\{2x-5y=-25②}\end{array}\right.$,
①×5-②×2得:11x=55,即x=5,
把x=5代入①得:y=7,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{13x+14y=41①}\\{14x+13y=40②}\end{array}\right.$,
①+②得:27(x+y)=81,即x+y=3③,
③×14-①得:x=1,
把x=1代入③得:y=2,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

| A. | 5 | B. | $\frac{1}{5}$ | C. | --$\frac{1}{5}$ | D. | -5 |
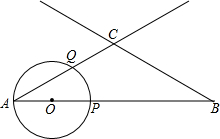 如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ.
如图,AB=3,∠A=∠B=30°,动点O从A出发,沿AB方向以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤1.5).以O为圆心,OA长为半径的⊙O与射线AB,AC的另一个交点分别为P,Q,连接CP,PQ. 如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM.
如图所示,在?ABCD中,AB=2BC,点M是DC的中点,BE⊥AD,E是垂足,求证:∠EMC=3∠DEM. 矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?
矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为多少?