题目内容
四张背面完全相同的纸牌(如图,用①、②、③、④表示),正面分别写有四个不同的条件.小明将这4张纸牌背面朝上洗匀后,先随机抽出一张(不放回),再随机抽出一张.

(1)写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);
(2)以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.

(1)写出两次摸牌出现的所有可能的结果(用①、②、③、④表示);
(2)以两次摸出的牌面上的结果为条件,求能判断四边形ABCD为平行四边形的概率.
考点:列表法与树状图法,平行四边形的判定
专题:
分析:(1)利用树状图展示所有等可能的结果数;
(2)由于共有12种等可能的结果数,根据平行四边形的判定能判断四边形ABCD为平行四边形有6种,则根据概率公式可得到能判断四边形ABCD为平行四边形的概率=
.
(2)由于共有12种等可能的结果数,根据平行四边形的判定能判断四边形ABCD为平行四边形有6种,则根据概率公式可得到能判断四边形ABCD为平行四边形的概率=
| 1 |
| 2 |
解答:解:(1)画树状图为:

(2)共有12种等可能的结果数,
其中能判断四边形ABCD为平行四边形有6种:①③、①④、②③、③①、③②、④①,
所以能判断四边形ABCD为平行四边形的概率=
=
.

(2)共有12种等可能的结果数,
其中能判断四边形ABCD为平行四边形有6种:①③、①④、②③、③①、③②、④①,
所以能判断四边形ABCD为平行四边形的概率=
| 6 |
| 12 |
| 1 |
| 2 |
点评:本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果数,再找出某事件所占有的结果数,然后根据概率公式计算这个事件的概率.也考查了平行四边形的判定.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 如图,在平面直角坐标系中,A是抛物线y=
如图,在平面直角坐标系中,A是抛物线y= 如图,一次函数y=ax+b与反比例函数y=
如图,一次函数y=ax+b与反比例函数y=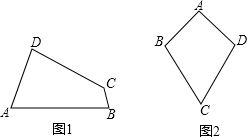 类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
 如图,在Rt△ABC中,∠ABC=90°,AC=10cm,点D为AC的中点,则BD=
如图,在Rt△ABC中,∠ABC=90°,AC=10cm,点D为AC的中点,则BD=