题目内容
7．先化简再求值：$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$-$\frac{{a}^{2}-2a}{a-2}$÷a，其中a=2．分析 先根据分式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．
解答 解：原式=$\frac{a+1}{a-1}$-a÷a
=$\frac{a+1}{a-1}$-1
=$\frac{a+1-（a-1）}{a-1}$
=$\frac{a+1-a+1}{a-1}$
=$\frac{2}{a-1}$，
当a=2时，原式=2．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
18．盐城市中学开展“唱红歌”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示．
（1）根据图示填写下表；
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；
（3）计算两班复赛成绩的方差．（方差公式：s2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
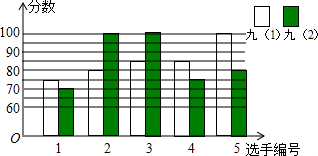
（1）根据图示填写下表；
| 班级 | 平均数（分） | 中位数（分） | 众数（分） |
| 九（1） | 85 | 85 | 85 |
| 九（2） | 85 | 80 | 100 |
（3）计算两班复赛成绩的方差．（方差公式：s2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．
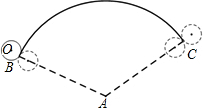如图，若弧BC的半径AB为12，圆心角为120°，半径为2的⊙O，从弧BC的一个端点B（切点）开始沿弧滚动到另一个端点C（切点），则⊙O需要转动2周．
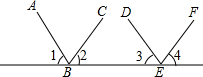完成下列推理说明：
如图，直线AB、CD、EF相交于点O．