题目内容
4.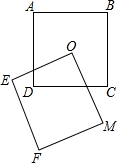 正方形ABCD与正方形OEFM的边长都等于1,且O点是正方形ABCD的对角线交点,现将正方形OEFM绕O点旋转,探究在旋转过程中两个正方形重叠部分的面积是否发生变化,为什么?如果没变化.那么面积是多少?
正方形ABCD与正方形OEFM的边长都等于1,且O点是正方形ABCD的对角线交点,现将正方形OEFM绕O点旋转,探究在旋转过程中两个正方形重叠部分的面积是否发生变化,为什么?如果没变化.那么面积是多少?
分析 根据正方形的性质得出OD=OC,∠ODG=∠OCH=45°,∠EOM=∠DOC=90°,得出∠DOG=∠COH,证出△ODG≌△OCH,即可得出结论.
解答 解:重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$,即面积为$\frac{1}{4}$×1×1=$\frac{1}{4}$,理由如下:
连接OD、OC,如图所示:
∵四边形ABCD和四边形OEFM都是正方形,边长为1,
∴OD=OC,∠ODG=∠OCH=45°,∠EOM=∠DOC=90°,
∴∠DOG=∠COH.
在△ODG与△OCH中,$\left\{\begin{array}{l}{∠ODG=∠OCH}&{\;}\\{OD=OC}&{\;}\\{∠DOG=∠COH}&{\;}\end{array}\right.$,
∴△ODG≌△OCH(ASA),
∴四边形OGDH的面积=△COD的面积,
∴重叠部分面积不变,总是等于正方形面积的$\frac{1}{4}$,
即$\frac{1}{4}$×1×1=$\frac{1}{4}$.
点评 本题考查了正方形的性质,全等三角形的性质和判定等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
14.太阳核聚变反应释放的辐射能功率为3.8×1023千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率用科学记数法表示为( )千瓦.
| A. | 1.9×1014 | B. | 2.0×1014 | C. | 7.6×1015 | D. | 1.9×1015 |
16.与算式23+23+23的运算结果相等的是( )
| A. | 23 | B. | 29 | C. | 3×23 | D. | 3×6 |
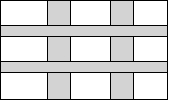 如图,在一块长为36米,宽为20米的矩形试验田中,计划挖两横、两竖四条水渠,横、竖水渠的宽度比为1:2,要使四条水渠所占面积是这块试验田面积的五分之一,求水渠的宽度.
如图,在一块长为36米,宽为20米的矩形试验田中,计划挖两横、两竖四条水渠,横、竖水渠的宽度比为1:2,要使四条水渠所占面积是这块试验田面积的五分之一,求水渠的宽度. 如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数.
如图,直线AB、CD相交于点O,OE平分∠AOD,∠DOE=30°,求∠BOC的度数.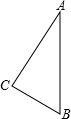 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为$\frac{84}{5}π$.
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为$\frac{84}{5}π$. 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=$\frac{4}{5}$.
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=$\frac{4}{5}$.