题目内容
9.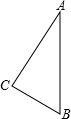 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为$\frac{84}{5}π$.
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,若把直角三角形绕边AB所在直线旋转一周,则所得几何体的表面积为$\frac{84}{5}π$.
分析 所得几何体的表面积为两个圆锥侧面积的和.
解答 解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设AB边上的高为h,则$\frac{1}{2}$×5h=$\frac{1}{2}$×3×4,
解得:h=$\frac{12}{5}$,
∴所得两个圆锥底面半径为$\frac{12}{5}$,
∴几何体的表面积=$\frac{1}{2}$×2π×$\frac{12}{5}$×4+$\frac{1}{2}$×2π×$\frac{12}{5}$×3=$\frac{84}{5}$π.
则所得几何体的表面积为$\frac{84}{5}π$.
点评 此题主要考查了圆锥的有关计算,正确确定旋转后的图形得出以AB边上的高为半径的圆的弧长是解题的关键.

练习册系列答案
相关题目
20.下面“去分母”后所得方程正确的是( )
| A. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=1 | |
| B. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2=x2-x | |
| C. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=x2-x | |
| D. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x(x-3)+2x=x-1 |
18.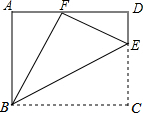 如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=$\frac{1}{3}$,求tan∠FBE的值.
 如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=$\frac{1}{3}$,求tan∠FBE的值.
19.用代数式表示:“x的5倍与y的和的一半”可以表示为( )
| A. | 5x+$\frac{1}{2}$y | B. | $\frac{1}{2}$ (5x+y) | C. | $\frac{1}{2}$(5x+2y) | D. | 5x+y. |
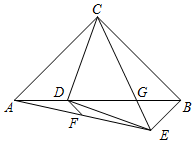 如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.
如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长2$\sqrt{2}$.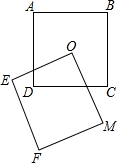 正方形ABCD与正方形OEFM的边长都等于1,且O点是正方形ABCD的对角线交点,现将正方形OEFM绕O点旋转,探究在旋转过程中两个正方形重叠部分的面积是否发生变化,为什么?如果没变化.那么面积是多少?
正方形ABCD与正方形OEFM的边长都等于1,且O点是正方形ABCD的对角线交点,现将正方形OEFM绕O点旋转,探究在旋转过程中两个正方形重叠部分的面积是否发生变化,为什么?如果没变化.那么面积是多少?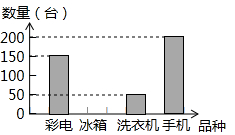 为扩大内需,国务院决定在全国实施“家电下乡”政策.第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品.我市一家家电商场,去年一季度对以上四种产品的销售情况进行了统计.结果显示冰箱销售的数量占总销量的20%,手机销售的数量占总销量的40%,并绘制了如图的条形统计图,请你解答下列问题:
为扩大内需,国务院决定在全国实施“家电下乡”政策.第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品.我市一家家电商场,去年一季度对以上四种产品的销售情况进行了统计.结果显示冰箱销售的数量占总销量的20%,手机销售的数量占总销量的40%,并绘制了如图的条形统计图,请你解答下列问题: 如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.
如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.