题目内容
12．超市以每瓶12元的价格购进一批洗面奶，销售一段时间后，为了获得更多的利润，超市决定提高价格销售，若按每瓶20元的价格销售，每月能卖120瓶；若按每瓶25元的价格销售，每月能卖70瓶；已知每月销售瓶数y（瓶）是每瓶销售价格x（元）的一次函数．每瓶洗面奶的销售价格定为多少元时，能使该月获得最大利润？分析 首先求出y与x的函数关系式，设每月的利润为P，构建二次函数，利用二次函数的性质即可解决问题．
解答 解：设y与x的函数关系式为y=kx+b，
由题意$\left\{\begin{array}{l}{20k+b=120}\\{25k+b=70}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-10}\\{b=320}\end{array}\right.$，
∴y与x的函数关系式为y=-10x+320．
设每月的利润为P，则P=（-10x+320）x-（-10x+320）×12
=-10x2+440x-3840，
∴x=$\frac{440}{-2×（-10）}$=22时，利润最大，
∴销售价格定为每瓶22元时，该月获得利润最大．
点评 本题考查二次函数的应用、一次函数的应用、待定系数法等知识，解题的关键是熟练掌握待定系数法，学会构建二次函数解决实际问题中的最值问题，属于中考常考题型．
练习册系列答案
相关题目
20．下面“去分母”后所得方程正确的是（ ）
| A． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2x=1 | |
| B． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2=x2-x | |
| C． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x-3+2x=x2-x | |
| D． | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1，去分母，得x（x-3）+2x=x-1 |
质量为10千克的物体G，从坡角为60°的坡面下滑（如图所示），已知AB=8米，物体G由点B下滑至点A，重力所做的功为392$\sqrt{3}$焦耳．（g取9.8，结果保留根号）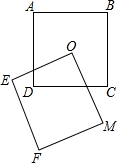
正方形ABCD与正方形OEFM的边长都等于1，且O点是正方形ABCD的对角线交点，现将正方形OEFM绕O点旋转，探究在旋转过程中两个正方形重叠部分的面积是否发生变化，为什么？如果没变化．那么面积是多少？
如图，一次函数y=ax+b的图象与反比例函数的图象交于A（-4，2），B（2，n）两点，且与x轴交于点C．
2．为了了解某县七年级学生的体重情况，从中抽取了200名学生进行体重测试，就这个问题，下面说法正确的是（ ）
| A． | 200名学生是总体 | B． | 200名学生是一个样本 | ||
| C． | 每个学生是个体 | D． | 全县七年级学生的体重是总体 |