Question

【题目】如图，将一个边长分别为8，16的矩形纸片ABCD沿EF折叠，使C点与A点重合，则EF与AF的比值为（ ）

A.4 B.C.2D.

Answer 1

【答案】B

【解析】

由折叠前后的两图形全等，得到一些线段相等，连接后转化到一个直角三角形中，由勾股定理可求出线段AF的长，由折叠A与C重合，折痕EF垂直平分AC，进而可以求出EF的长，最后再求EF与AF的比值．

连接AC交EF于点O，连接FC，

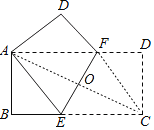
由折叠得：AF=FC，EF垂直平分AC，

设AF=x，则DF=16-x

在Rt△CDF中，由勾股定理得：

DF2+CD2=FC2，

即：（16-x）2+82=x2，解得：x=10，

在Rt△ABC中，由勾股定理得：

AC=，

∴OA=CO=4，

在Rt△FOC中，OF=，

EF=2OF=4，

∴，

故选B．