题目内容
7.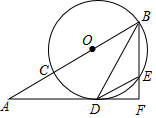 过⊙O的直径BC的延长线上一点A作圆的切线,D为切点,过B作切线的垂线交圆于点E,F为垂足,AC=DE,求AC和AB的比值.
过⊙O的直径BC的延长线上一点A作圆的切线,D为切点,过B作切线的垂线交圆于点E,F为垂足,AC=DE,求AC和AB的比值.
分析 解:连结OD、CD,如图,利用切线的性质得OD⊥AF,则OD∥BF,所以∠1=∠2,则可证明∠2=∠3得到CD=DE,加上AC=DE,所以AC=CD,接着证明△OCD为等边三角形得到∠6=60°,CD=OC,所以AO=2OD=2CD=2AC,然后计算AC:AB的值.
解答 解:连结OD、CD,如图,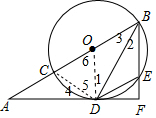
∵AF为切线,
∴OD⊥AF,
∵BF⊥AF,
∴OD∥BF,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴$\widehat{CD}$=$\widehat{DE}$,
∴CD=DE,
而AC=DE,
∴AC=CD,
∴∠A=∠4,
∵∠A+∠6=90°,∠4+∠5=90°,
∴∠5=∠6,
∴CO=CD,
而OC=OD,
∴△OCD为等边三角形,
∴∠6=60°,CD=OC,
∴AO=2OD=2CD=2AC,
∴AC:AB=AC:3AC=1:3.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决本题的判断△OCD为等边三角形.

练习册系列答案
相关题目
20.用代数式表示“m的3倍与n的平方差”,正确的是( )
| A. | (3m-n)2 | B. | 3(m-n)2 | C. | (3m)2-n2 | D. | (m-3n)2 |
18.下列说法中正确的个数有( )
①0是绝对值最小的有理数;
②无限小数是无理数;
③数轴上原点两侧的数互为相反数;
④a,0,$\frac{1}{x}$都是单项式;
⑤-3x2y+4x-1是关于x,y的三次三项式,常数项是-1.
①0是绝对值最小的有理数;
②无限小数是无理数;
③数轴上原点两侧的数互为相反数;
④a,0,$\frac{1}{x}$都是单项式;
⑤-3x2y+4x-1是关于x,y的三次三项式,常数项是-1.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.二次函数y=$\frac{1}{2}$x2-6x+21的顶点坐标是( )
| A. | (-6,3) | B. | (-6,21) | C. | (6,3) | D. | (6,21) |
 如图,在△ABC中,点D是AB上的一点,作DE∥BC交AC于点E,连接CD、BE交于点G,取BC的中点F,并连接FG,则图中三角形面积一定相等的有( )
如图,在△ABC中,点D是AB上的一点,作DE∥BC交AC于点E,连接CD、BE交于点G,取BC的中点F,并连接FG,则图中三角形面积一定相等的有( )