题目内容
8.计算(1)$\frac{3}{x+1}$+$\frac{3x}{x+1}$
(2)x3•x4•x+(x2)4+(-2x4)2
(3)因式分解:3m3n2-6m2n3+3mn4
(4)解分式方程:$\frac{2x}{x+3}$+1=$\frac{7}{2x+6}$.
分析 (1)原式利用同分母分式的加法法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(3)原式提取公因式,再利用完全平方公式分解即可;
(4)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{3(x+1)}{x+1}$=3;
(2)原式=x8+x8+4x8=6x8;
(3)原式=3mn2(m2-2mn+n2)=3mn2(m-n)2;
(4)去分母得:4x+2x+6=7,
解得:x=$\frac{1}{6}$,
经检验x=$\frac{1}{6}$是分式方程的解.
点评 此题考查了解分式方程,整式的混合运算,提公因式法与公式法的综合运用,以及分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
10.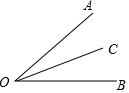 如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
 如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )
如图,OC为∠AOB内一条射线,下列条件中能确定OC平分∠AOB的是( )| A. | ∠BOC=$\frac{1}{2}$∠AOC | B. | ∠AOC+∠COB=∠AOB | C. | ∠AOB=2∠AOC | D. | ∠COB=∠AOB-∠AOC |
11.在长度分别为4厘米、5厘米、9厘米、12厘米的四条线段中,任选三条线段可以组成三角形的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

 如图,是一个数值转换机的示意图.若输出的结果是6,则输入的数等于5或-7.
如图,是一个数值转换机的示意图.若输出的结果是6,则输入的数等于5或-7.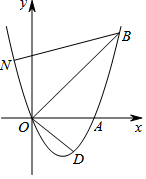 如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.
如图,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.