题目内容
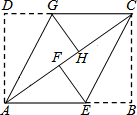 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,其中F,H分别是B,D的落点.求证:四边形AECG是平行四边形.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC,AD恰好落在AC上,其中F,H分别是B,D的落点.求证:四边形AECG是平行四边形.考点:平行四边形的判定,翻折变换(折叠问题)
专题:证明题
分析:利用翻折变换的性质得出2∠GAH=∠DAC,2∠ECF=∠BCA,进而得出AG∥CE求出即可.
解答:证明:在矩形ABCD中,
∵AD∥BC,∴∠DAC=∠BCA.
由已知得:2∠GAH=∠DAC,
2∠ECF=∠BCA,
∴∠GAH=∠ECF.∴AG∥CE
又∵AE∥CG,
∴四边形AECG是平行四边形.
∵AD∥BC,∴∠DAC=∠BCA.
由已知得:2∠GAH=∠DAC,
2∠ECF=∠BCA,
∴∠GAH=∠ECF.∴AG∥CE
又∵AE∥CG,
∴四边形AECG是平行四边形.
点评:此题主要考查了平行四边形的判定以及翻折变换的性质,得出∠GAH=∠ECF是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等腰三角形底边长是10,周长是40,则其底角的正弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知-1≤a≤1,则x2+(a-4)x+4-2a>0的解为( )
| A、x>3或x<2 |
| B、x>2或x<1 |
| C、x>3或x<1 |
| D、1<x<3 |
化简:-
=( )
| 4 |
| A、2 | B、-2 | C、4 | D、-4 |
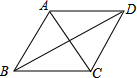 如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为
如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠BDC的度数为