题目内容
下列方程:①x2+1=0;②2y(3y-5)=6y2+4;③(x-2)(x-3)=5;④
x=
x2;⑤
-1=0;⑥
=1,其中一元二次方程的个数为( )
| 3 |
| 2 |
| 1+x2 |
| 2 |
| 2 |
| 1+x2 |
| A、2 | B、3 | C、4 | D、5 |
考点:一元二次方程的定义
专题:
分析:本题根据一元二次方程的定义解答.
一元二次方程必须满足四个条件:
(1)未知数的最高次数是2;
(2)二次项系数不为0;
(3)是整式方程;
(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
一元二次方程必须满足四个条件:
(1)未知数的最高次数是2;
(2)二次项系数不为0;
(3)是整式方程;
(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
解答:解:①x2+1=0是一元二次方程;
②2y(3y-5)=6y2+4是一元一次方程;
③(x-2)(x-3)=5是一元二次方程;
④
x=
x2是一元二次方程;
⑤
-1=0是一元二次方程;
⑥
=1是分式方程,
故选:C.
②2y(3y-5)=6y2+4是一元一次方程;
③(x-2)(x-3)=5是一元二次方程;
④
| 3 |
| 2 |
⑤
| 1+x2 |
| 2 |
⑥
| 2 |
| 1+x2 |
故选:C.
点评:本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.

练习册系列答案
相关题目
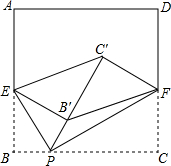 如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.
如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.