Question

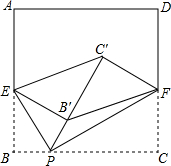如图，已知，正方形纸片ABCD的边长为4，点P在BC边上，BP=1，点E在AB边上，且∠BPE=60°，沿PE翻折△EBP得到△EB′P． F是CD边上一点，沿PF翻折△FCP得到△FC′P，使点Cˊ落在射线PBˊ上．
（1）求证：EB′∥C′F；
（2）连接B′F、C′E，求证：四边形EB′F C′是平行四边形．

Answer 1

考点：正方形的性质,平行四边形的判定,翻折变换（折叠问题）

专题：

分析：（1）证明∠EB′C′=90°；∠FC′P=90°，得到∠EB′C′=∠FC′P，即可解决问题．
（2）证明EB′=FC′；结合EB′∥C′F，即可解决问题．

解答：证明：（1）∵四边形ABCD是正方形，
∴∠B=∠C=90°．
∵沿PE翻折△EBP得到△EB′P，
∴∠EB′P=∠B=90°．即∠EB′C′=90°；
∵沿PF翻折△FCP得到△FC′P，
∴∠FC′P=∠C=90°；
∴∠EB′C′=∠FC′P，
∴EB′∥C′F．
（2）在Rt△EBP中，
∵∠BPE=60°，BP=1，
∴BE=

3

．
∵沿PE翻折△EBP得到△EB′P，沿PF翻折△FCP得到△FC′P，
∴∠FPC=30°；
∵BC=4，BP=1，
∴PC=3，FC=

3

．
∴BE=FC；即EB′=FC′；
又∵EB′∥C′F，
∴四边形EB′F C′是平行四边形．

点评：该题主要考查了正方形的性质、平行四边形的判定、直角三角形的边角关系等几何知识点及其应用问题；解题的关键是牢固掌握有关判定定理，并内灵活运用．