题目内容
已知x、y为直角三角形的两边的长,满足
+|y2-5y+6|=0,则第三边的长为 .
| x2-4 |
考点:勾股定理,非负数的性质:绝对值,非负数的性质:算术平方根
专题:分类讨论
分析:首先利用绝对值以及算术平方根的性质得出x,y的值,再利用分类讨论结合勾股定理求出第三边长.
解答:解:∵x、y为直角三角形的两边的长,满足
+|y2-5y+6|=0,
∴x2-4=0,y2-5y+6=0,
解得:x1=2,x2=-2(不合题意舍去),y1=2,y2=3,
当直角边长为:2,2,则第三边长为:2
,
当直角边长为:2,3,则第三边长为:
,
当直角边长为2,斜边长为3,则第三边长为:
.
故答案为:2
,
或
.
| x2-4 |
∴x2-4=0,y2-5y+6=0,
解得:x1=2,x2=-2(不合题意舍去),y1=2,y2=3,
当直角边长为:2,2,则第三边长为:2
| 2 |
当直角边长为:2,3,则第三边长为:
| 13 |
当直角边长为2,斜边长为3,则第三边长为:
| 5 |
故答案为:2
| 2 |
| 5 |
| 13 |
点评:此题主要考查了勾股定理以及绝对值以及算术平方根的性质,正确应用勾股定理是解题关键.

练习册系列答案
相关题目
下列各单项式中,不是同类项的是( )
| A、0和-9 | ||||
B、
| ||||
| C、5xy2和-y2x | ||||
| D、2m2n3和3m3n2 |
 有理数a、b在数轴上的位置如图所示,化简|a+1|+|1-b|的值为( )
有理数a、b在数轴上的位置如图所示,化简|a+1|+|1-b|的值为( )| A、a+b | B、a-b+2 |
| C、-a-b | D、b-a-2 |
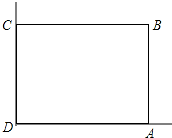 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.