Question

3．在ABC中，∠ACB=90°，∠B=60°，AC=6，点D，E在AB边上，AD=CD，点E关于AC，CD的对称点分别为F，G，则线段FG的最小值等于（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 根据轴对称的性质得出CE=CF，∠CEF=∠CFE，CE=CG，EH=GH，∠CEF=∠CGH，进而得出CE=CG=CF，∠CGH=∠CFE，然后证得△BCD是等边三角形，从而证得∠FHG=60°，进一步证得∠FCG=∠FHG=60°，证得△CFG是等边三角形，得出FG=CF=CE，因为CE的最小值为3，所以FG的最小值为3．

解答 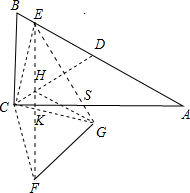解：∵点E和F关于AC对称，
∴AC垂直平分EF，
∴CE=CF，∠CEF=∠CFE，
∵点E和G关于CD对称，
∴CD垂直平分FG，
∴CE=CG，EH=GH，∠CEF=∠CGH，
∴CE=CG=CF，∠CGH=∠CFE，
∵∠ACB=90°，∠B=60°，
∴∠A=30°，
∵AD=CD，
∴∠ACD=∠A=30°，
∴∠BCD=60°，
∴△BCD是等边三角形，
∵EF∥BC，
∴∠DEH=∠B=60°，∠EHD=∠BCD=60°，
∴∠DHG=∠EHD=60°，
∴∠FHG=60°
∵∠CGH=∠CFE，∠CKF=∠HKG，
∴∠FCG=∠FHG=60°，
∵CF=CG，
∴△CFG是等边三角形，
∴FG=CF=CE，
∵当CE⊥AB时，CE最短，此时CE=$\frac{1}{2}$AC=3，
∴FG的最小值为3，
故选B．

点评 本题考查了轴对称的性质和等边三角形的判定和性质，证得△CFG是等边三角形是解题的关键．