题目内容
16.已知下列命题:①方程x+$\frac{5}{x}$=6的解是x=5;
②有两边和一角对应相等的两个三角形全等;
③二次函数y=x2-2mx+2m-2的顶点在x轴下方;
④对角线相等,互相垂直其平分的四边形是正方形
其中真命题为④.
分析 利用分式方程的解法以及全等三角形的判定方法和正方形的判定方法进而分析得出即可.
解答 解:①方程x+$\frac{5}{x}$=6的解是:x1=1,x2=5,故此选项错误;
②有两边和一角对应相等的两个三角形全等,故此选项错误;
③二次函数y=x2-2mx+2m-2的顶点在x轴下方,$\frac{{b}^{2}-4ac}{4a}$=$\frac{(2m)^{2}-4×(2m-2)}{4×1}$=(m-1)2+1>0,
则二次函数y=x2-2mx+2m-2的顶点在x轴上方,故此选线错误;
④对角线相等,互相垂直其平分的四边形是正方形,正确.
故答案为:④.
点评 此题主要考查了命题与定理,正确把握相关定义是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
 如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )| A. | 6$\sqrt{3}$米 | B. | 6米 | C. | 3$\sqrt{3}$米 | D. | 3米 |

 某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升7.09元.
某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升7.09元.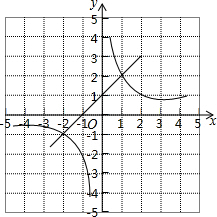 一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.
一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1. 甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )
甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )