题目内容
6．如图所示的运算程序中，若开始输入的x值为48，我们发现第一次输出的结果为24，第二次输出的结果为12，…，则第2010次输出的结果为（ ）
| A． | 6 | B． | 4 | C． | 3 | D． | 1 |
分析 把x的值代入程序中计算，以此类推得到一般性规律，即可得到第2010次输出结果．
解答 解：把x=48代入程序中得：$\frac{1}{2}$×48=24，
把x=24代入程序中得：$\frac{1}{2}$×24=12，
把x=12代入程序中得：$\frac{1}{2}$×12=6，
把x=6代入程序中得：$\frac{1}{2}$×6=3，
把x=3代入程序中得：x+3=6，
除去前两项，依次以3，6循环，
∵（2010-2）÷2=1004，
∴第2010次输出的结果为3，
故选：C．
点评 此题考查了代数式求值，弄清题中程序框图表示的意义是解本题的关键．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
16．下列式子中，计算正确的是（ ）
| A． | -$\sqrt{3.6}$=-0.6 | B． | $\sqrt{（-13）^{2}}$=-13 | C． | $\sqrt{36}$=±6 | D． | -$\sqrt{9}$=-3 |
17．任意给定一个非零数，按如图程序计算，最后输出的结果（ ）
| A． | m | B． | m2 | C． | m+1 | D． | m-1 |
如图，AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于C，AB=6cm，PB=8cm，则BC=4.8cm．
11．
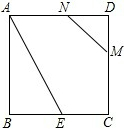如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（ ）时，△ABE与以D、M、N为顶点的三角形相似．
如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（ ）时，△ABE与以D、M、N为顶点的三角形相似．| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{5}}}{5}$或$\frac{{2\sqrt{5}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$或$\frac{{3\sqrt{5}}}{5}$ |
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论中正确结论的个数是（ ）