题目内容
14. 如图,⊙O中,如果∠AOB=2∠COD,那么( )
如图,⊙O中,如果∠AOB=2∠COD,那么( )| A. | AB=DC | B. | AB<DC | C. | AB<2DC | D. | AB>2DC |
分析 过点O作OE⊥AB交⊙O于点E,连接AE、BE,可得∠AOE=∠BOE=$\frac{1}{2}$∠AOB,根据∠COD=$\frac{1}{2}$∠AOB,知∠AOE=∠BOE=∠COD,即CD=AE=BE,在△ABE中,由AE+BE>AB可得2CD>AB.
解答 解:如图,过点O作OE⊥AB交⊙O于点E,连接AE、BE,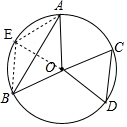
∴∠AOE=∠BOE=$\frac{1}{2}$∠AOB,
又∵∠COD=$\frac{1}{2}$∠AOB,
∴∠AOE=∠BOE=∠COD,
∴CD=AE=BE,
∵在△ABE中,AE+BE>AB,
∴2CD>AB,
故选:C.
点评 本题主要考查垂径定理和圆心角定理,根据∠AOB=2∠COD利用垂径定理将角平分,从而根据圆心角定理得出答案是解题的关键.

练习册系列答案
相关题目
5.如果“爱”、“我”、“中”、“华”这四个汉字分别代表一个非零个位数,对于运算符号“★”有:爱我中华★1=我爱中华:爱我中华★2=中华我爱,那么1234★1★2=( )
| A. | 4312 | B. | 3412 | C. | 4321 | D. | 3421 |
9.有理数a、b满足a2b2+a2+b2-4ab+1=0,则a、b的值分别为( )
| A. | a=1,b=1 | B. | a=-1,b=-1 | C. | a=b=1或a=b=-1 | D. | 不能确定 |
6.平面图形的旋转一般情况下改变图形的是( )
| A. | 位置 | B. | 大小 | C. | 形状 | D. | 性质 |





 如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.