题目内容
3.在反比例函数y=-$\frac{2}{x}$的图象上有两点(-$\frac{1}{2}$,y1),(-2,y2),则y1-y2的值是( )| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 不能确定 |
分析 直接把各点坐标代入反比例函数的解析式,再求出其差即可.
解答 解:∵反比例函数y=-$\frac{2}{x}$的图象上有两点(-$\frac{1}{2}$,y1),(-2,y2),
∴y1=-$\frac{2}{-\frac{1}{2}}$=4,y2=-$\frac{2}{-2}$=1,
∴y1-y2=4-1=3.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.矩形具有而一般的平行四边形不一定具有的特征( )
| A. | 对角相等 | B. | 对角线相等 | C. | 对角线互相平分 | D. | 对边相等 |
18.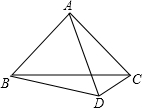 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )| A. | 30° | B. | 15° | C. | 45° | D. | 35° |
8.比-1小2015的数是( )
| A. | -2014 | B. | 2016 | C. | -2016 | D. | 2014 |
15.不等式$\left\{\begin{array}{l}{-x<3}\\{4x-8≤12}\end{array}\right.$的解集是( )
| A. | -3<x≤5 | B. | 3<x≤5 | C. | 3<x≤-5 | D. | -3<x<5 |
12.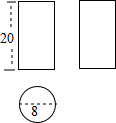 如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
 如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )
如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)( )| A. | 128πcm2 | B. | 160πcm2 | C. | 176πcm2 | D. | 192πcm2 |