题目内容
8.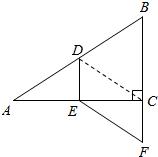 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由三角形中位线定理得出DE∥BC,由直角三角形斜边上的中线性质得出CD=$\frac{1}{2}$AB=AD=BD,又CF=$\frac{1}{2}$BC,即可证出四边形CDEF是平行四边形,由此即可解决问题.
解答  解:∵AD=DB,AE=EC,
解:∵AD=DB,AE=EC,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∵CF=$\frac{1}{2}$BC,
∴DF∥CF,DF=CF,
∴四边形DEFC是平行四边形,
∴EF=CD,
∵∠ACB=90°,AD=DB,AB=10,
∴CD=$\frac{1}{2}$AB=5,
∴EF=5.
故选A.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
6.下列长度的线段能组成三角形的是( )
| A. | 3,4,7 | B. | 3,3,6 | C. | 2,5,8 | D. | 6,7,8 |
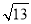 <n,则mn的平方根 =__.
<n,则mn的平方根 =__.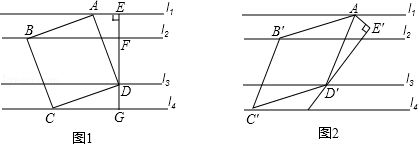

 如图,已知△ABC的三个顶点的坐标分别为:A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为:A(-2,3)、B(-6,0)、C(-1,0).